Ângulo Sólido
Ângulo Sólido
Quando estudamos trigonometria aprendemos que o comprimento $C$ de uma circunferência de raio $r$ é dada por $C=2\pi r$, ou seja, $C$ é o produto do comprimento máximo de arco unitário $\theta_{max}=2\pi$ pelo raio $r$. Se queremos uma fração $l$ do comprimento de arco da circunferência de raio $r$ basta escolher um valor de $\theta$ contido no intervalo $0\leqslant\theta\leqslant2\pi$ de modo que podemos escrever $l=\theta r$, o que nos proporciona a expressão para o ângulo formado pelo comprimento de arco $l$ a uma distância $r$ da origem da circunferência $\theta=\frac{l}{r}.$ Note que $\theta$ é diretamente proporcional a $l$, logo se tomarmos uma quantidade infinitesimal $d\theta$ do ângulo teremos um arco infinitesimal $dl$ como ilustra a figura abaixo, dessa forma um ângulo infinitesimal $d\theta$ é dado pela expressão $$d\theta=\frac{dl}{r}.$$Um ângulo sólido é uma generalização tridimensional do conceito bidimensional de comprimento de arco de circunferência unitária (ângulo). Sendo uma superfície esférica a extensão natural de uma circunferência é razoável considerar a área superficial como a extensão natural do comprimento de arco. Da geometria elementar obtemos que a área de uma casca esférica de raio $r$ é dada por $A=4\pi r^2$, de forma análoga ao caso bidimensional se considerarmos $4\pi=\Omega_{max}$ como a área de uma esfera de raio unitário centrada dentro da esfera de raio $r$ podemos descrever uma fração da área $A$ considerando um valor de $\Omega$ contido no intervalo $0\leqslant \Omega\leqslant4\pi$ de modo que essa fração da área da esfera de raio $r$ pode ser escrita da seguinte forma $A=\Omega r^2$. A área $\Omega$ é o análogo tridimensional de $\theta$, que recebe o nome de ângulo sólido o qual pode ser identificado em sua forma infinitesimal na figura abaixo,
logo um ângulo sólido infinitesimal pode ser escrito da seguinte forma
$$d\Omega=\frac{dA}{r^2}. \ \ \ \ \ \ \ (1)$$ O ângulo sólido também pode ser escrito considerando o versor de $\vec{r}=\frac{\vec{r}}{r}=\hat{r}$ ortogonal a superfície $d\Omega$ e um vetor unitário $\hat{n}$ ortogonal a $dA$ de modo que $d\vec{A}=\hat{n}dA$, assim escrevemos $$d\Omega=\frac{\hat{r}\cdot d\vec{A}}{r^2}.$$
Note que construímos toda nossa argumentação para um ângulo sólido centrado dentro da esfera de modo que $\Omega$ varre a esfera por completo, o que implica que ao integrar em toda a superfície obtemos $$\oint d\Omega=\frac{4\pi r^2}{r^2}=4\pi;\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Dentro\ da\ superfície.$$ O mesmo não é valido para um ângulo sólido centrado fora da superfície esférica, como ilustrado na figura abaixo,
pois para um $d\Omega$ muito pequeno $dA=dA'$ e sendo $\hat{n}'=-\hat{n}$ as quantidades $dA$ e $dA'$ dão contribuições opostas que se cancelam.
$$\oint d\Omega=0;\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ Fora\ da\ superfície.$$
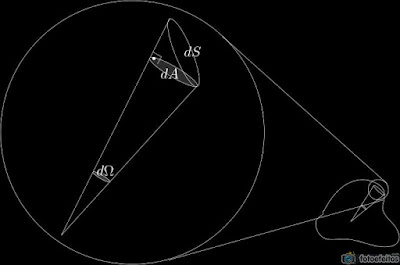
Podemos usar a definição de ângulo sólido que acabamos de construir para varrer qualquer superfície de área $S$. No limite em que $\Omega$ é muito pequeno a área $dA$ se aproxima da área $dS$.
Nesse limite $dA$ e $dS$ são aproximadamente planos de modo que se for possível relacionar às duas superfícies podemos usar a equação (1) para encontras a relação entre $dS$ e $d\Omega$. Note que $dA$ é um círculo, vez que é a cônica obtida através de um corte reto de um cone, já $dS$ é uma elipse, já que é uma cônica obtida por um corte transversal no cone. As áreas dessas duas figuras são conhecidas o que nos da $dA=\pi c^2$ e $dS=\pi ab$, onde $c$ é o raio da circunferência e $a$ e $b$ são respectivamente os raios menor e maior da elipse.
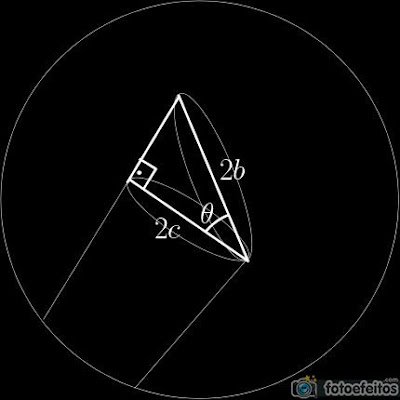
O nosso problema se resume agora a encontrar uma relação entre $c$ e $a$, $b$ de modo a relacionar $dA$ e $dS$. Note que $c=a$ no limite em que $\Omega$ tende a $d\Omega$, pois o cone se aproxima de um cilindro. A relação entre $c$ e $b$ é obtida ao perceber que nesse limite às duas figuras, $dA$ e $dS$, formam um triangulo retângulo, mais especificamente seus diâmetros,
dessa forma usando relações entre cossenos obtemos $b=\frac{c}{\cos\theta}$. Dessa relação obtemos $dS=\frac{\pi c^2}{\cos\theta}\ \ \Rightarrow\ \ c^2=\frac{dS\cos\theta}{\pi}$, logo sendo $dA=\pi c^2$ teremos $$dA=dS\cos\theta.\ \ \ \ \ \ \ \ \ (2)$$
Substituindo a equação (2) em (1) obtemos
$$d\Omega=\frac{dS\cos\theta}{r^2}.$$
Como antes podemos considerar $\hat{n}$ ortogonal a $dS$ e $\hat{r}$ a $dA$ para escrever a expressão de forma vetorial, basta notar que $\theta$ também é o ângulo formado por esses vetores,
$$d\Omega=\frac{\hat{r}\cdot d\vec{S}}{r^2}.$$
onde finalmente teremos






Comentários