Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 2.12

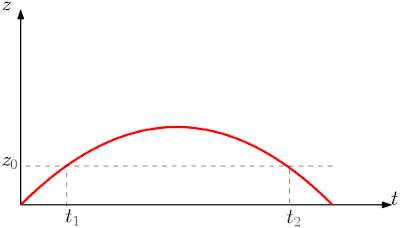
12) Um método possível para medir a aceleração da gravidar $g$ consiste em lançar uma bola para cima num tubo com vácuo e medir a passagem da bolinha em uma distância $z$ nos instantes $t_1$ e $t_2$ de passagem da bolinha por essa altura $z$ mostre que

$$g=\frac{2z}{t_1t_2}$$

Sabemos que a equação que descreve o movimento de lançamento vertical é $$z=z_0+v_0t-\frac{1}{2}gt^2$$ porem como a bolinha foi lançada da base do cilindro teremos que $$z=v_0t-\frac{1}{2}gt^2$$ nos instantes $t_1$ e $t_2$ a bolinha passa pela posição $z_0$ logo teremos que $$\left\lbrace \begin{array}{ll} z_0=v_0t_1-\frac{1}{2}gt_1^2\\ z_0=v_0t_2-\frac{1}{2}gt_2^2 \end{array}\right. \ \ \ \ (1)$$ Podemos agora comparar às duas equações igualando $z_0$ dessa forma obtemos $$v_0t_2-\frac{1}{2}gt_2^2=v_0t_1-\frac{1}{2}gt_1^2$$ explicitando $v_0$ obtemos que $$v_0\left( t_1-t_2\right)=\frac{1}{2}g\left( t_1^2-t_2^2\right) \Rightarrow$$ $$v_0\left( t_1-t_2\right)=\frac{1}{2}g\left( t_1-t_2\right)\left( t_1+t_2\right) \Rightarrow $$ $$v_0=\frac{1}{2}g\left( t_1+t_2\right)\ \ \ \ (2)$$ Substituindo a expressão $(2)$ em $(1)$ obtemos $$z_0=\frac{1}{2}g\left( t_1+t_2\right)t_2-\frac{1}{2}gt_2^2\Rightarrow$$ $$z_0=\frac{1}{2}gt_1t_2+\frac{1}{2}gt_2^2-\frac{1}{2}gt_2^2\Rightarrow$$ $$z_0=\frac{1}{2}gt_1t_2\Rightarrow$$ $$g=\frac{2z_0}{t_1t_2}$$