Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 9.14
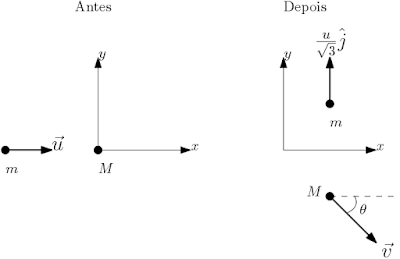
9.14) Uma partícula de massa $m$ e velocidade $\vec{u}$ colide elasticamente com outra de massa $M$, inicialmente em repouso no referencial do laboratório. Após a colisão, a partícula de massa $m$ foi defletida em um ângulo de 90°, e a magnitude da sua velocidade foi reduzida para $u/\sqrt{3}$, onde $u=|\vec{u}|$. A partícula de massa $M$ emerge da colisão com velocidade $v$, numa direção que faz um ângulo $\theta$ com $\vec{u}$. (a) Determine $\theta$; (b) Calcule a razão de $\lambda=\frac{M}{m}$ e a velocidade $v$. (c) Determine os ângulos $\theta'_m$ e $\theta'_M$ entre as direções de movimento final de $m$ e $M$, respectivamente, e a direção de $\vec{u}$, no referencial do CM.
(a) No referencial do laboratório teremos o seguinte diagrama de antes e depois da colisão,a partir dessa informações podemos usar a conservação de momento para obter a seguinte equação vetorial, $$\vec{P}_{im}=\vec{P}_{fm}+\vec{P}_{fM}\Rightarrow$$ $$mu\hat{i}=\frac{1}{\sqrt{3}}mu\hat{j}+M\vec{v}$$ Tal equação resulta nas seguinte equações escalares, $$\left\lbrace \begin{array}{ll} mu=Mv\cos\theta\\ 0=\frac{1}{\sqrt{3}}mu-Mv\sin\theta \end{array}\right.$$ isolando $\sin\theta$ e $\cos\theta$ obtemos, $$\left\lbrace \begin{array}{ll} \sin\theta=\frac{1}{\sqrt{3}}\frac{mu}{Mv}\ \ \ \ \ \ (1)\\ \cos\theta=\frac{mu}{Mv}\ \ \ \ \ \ (2) \end{array}\right.$$ dividindo a primeira equação pela segunda obtemos, $$\tan\theta=\frac{1}{\sqrt{3}}\Rightarrow$$ $$\theta=\arctan\left( \frac{1}{\sqrt{3}}\right)\Rightarrow$$ $$\theta=-30°$$ (b) Olhando para a conservação de energia do sistema, temos que, $$\frac{1}{2}mu^2=\frac{1}{2}m\left(\frac{1}{\sqrt{3}}u\right)^2+\frac{1}{2}Mv^2 \Rightarrow$$ $$mu^2=\frac{1}{3}mu^2+Mv^2 \Rightarrow$$ $$\left( \frac{u}{v}\right)^2=\frac{3}{2}\frac{M}{m}\ \ \ \ (3)$$ Elevando (2) ao quadrado e substituindo (3) em (2) obtemos, $$\cos^2\theta=\left( \frac{m}{M}\right)^2\left( \frac{3}{2}\frac{M}{m}\right) $$ como $\theta=30°$ teremos, $$\frac{3}{4}=\frac{3}{2}\frac{m}{M}\Rightarrow $$ $$\frac{M}{m}=2\ \ \ \ \ (4)$$ aplicando (4) novamente em (2) obtemos, $$v=\frac{1}{\sqrt{3}}u \ \ \ \ \ (5)$$ (c) Os vetores velocidades finais $\vec{v}_{fm}$ e $\vec{v}_{fM}$ em relação ao referencial do laboratório são, $$\left\lbrace \begin{array}{ll} \vec{v}_{fm}=\frac{u}{\sqrt{3}}\hat{j}\\ \vec{v}_{fM}=v\cos\theta\hat{i}-v\sin\theta\hat{j} \end{array}\right. $$ sabendo que $\theta=30°$ e sabendo o valor da velocidade final de $M$ dado pela equação (5) $$\left\lbrace \begin{array}{ll} \vec{v}_{fm}=\frac{u}{\sqrt{3}}\hat{j}\ \ \ \ \ \ (6)\\ \vec{v}_{fM}=\frac{u}{2}\hat{i}-\frac{\sqrt{3}}{6}u\hat{j}\ \ \ \ \ \ (7) \end{array}\right. $$ usando as equações (6) e (7) podemos calcular a velocidade do centro de massa, $$\vec{V}_{cm}=\frac{m\vec{v}_{fm}+M\vec{v}_{fM}}{m+M}\Rightarrow$$ $$\vec{V}_{cm}=\frac{m\frac{u}{\sqrt{3}}\hat{j}+M\left(\frac{u}{2}\hat{i}-\frac{\sqrt{3}}{6}u\hat{j} \right) }{m+M}\Rightarrow$$ $$\vec{V}_{cm}=\frac{Mu}{2\left(M+m\right) }\hat{i}+\frac{\sqrt{3}}{M+m}\left( \frac{2m-M}{6}\right)u\hat{j} $$ lembrando que $m=\frac{1}{2}M$ obtemos, $$\vec{V}_{cm}=\frac{1}{3}u\hat{i}\ \ \ \ \ \ (8)$$ Usando agora a Transformação de Galileu obtemos, $$\left\lbrace \begin{array}{ll} \vec{v}'_{fm}=\vec{v}_{fm}-\vec{V}_{cm}\\ \vec{v}'_{fM}=\vec{v}_{fM}-\vec{V}_{cm} \end{array}\right. \Rightarrow$$ $$\left\lbrace \begin{array}{ll} \vec{v}'_{fm}=\frac{\sqrt{3}}{3}u\hat{j}-\frac{u}{3}\hat{i}\\ \vec{v}'_{fM}=\frac{u}{6}\hat{i}-\frac{\sqrt{3}u}{6}\hat{j} \end{array}\right. \Rightarrow$$ dessa forma podemos calcular o ângulo entre esses vetores e a vertical $\hat{i}$, $$\left\lbrace \begin{array}{ll} \cos\theta'_m=\frac{\vec{v}'_m\cdot\hat{i}}{|\vec{v}'_m||\hat{i}|}\\ \cos\theta'_M=\frac{\vec{v}'_M\cdot\hat{i}}{|\vec{v}'_M||\hat{i}|} \end{array}\right. $$ Realizando os devidos cálculos encontramos que, $$\left\lbrace \begin{array}{ll} \cos\theta'_m=-\frac{1}{2}\\ \cos\theta'_M=\frac{1}{2} \end{array}\right. $$ ou seja, $$\left\lbrace \begin{array}{ll} \theta'_m=\arccos\left( -\frac{1}{2}\right) \\ \theta'_M=\arccos\left( \frac{1}{2}\right) \end{array}\right. \Rightarrow$$ $$\left\lbrace \begin{array}{ll} \theta'_m=120° \\ \theta'_M=300° \end{array}\right. $$


Comentários