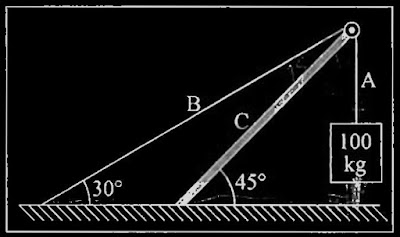
3) No sistema representado na figura, calcule as Tensões nas cordas $A$ e $B$ a compressão na viga $C$, desprezando as massas da viga e das cordas.
Adotando o referencial no ponto onde a corda entra em contato com a viga podemos representar as forças que atuam sobre o sistema da seguinte forma, a corda faz uma pressão sobre a viga gerando uma força normal $\vec{N}$ que faz um ângulo $\varphi$ com a vertical, existe uma tração $\vec{T}_A$ na vertical e outra $\vec{T}_B$ fazendo um angulo $\theta$ com a vertical e a corda $B$. Tal situação pode ser representada na figura a baixo

Pela segunda lei de Newton teremos que
$$\sum\vec{F}=\vec{N}+\vec{T}_A+\vec{T}_B$$
decompor as forças na direção vertical e horizontal, como o sistema está em equilíbrio as forças resultantes na direção $x$ e $y$ devem ser nulas, dessa forma obtemos às duas equações escalares
$$\left\lbrace \begin{array}{ll}
N_x-T_{Bx}=0\\
N_y-T_A-T_{By}=0
\end{array}\right. $$
Note que as forças que atuam sobre o bloco são apenas $\vec{T}_A=-\vec{P}$ logo
$$\left\lbrace \begin{array}{ll}
N\cos\varphi-T_{B}\sin\theta=0\ \ \ \ (1)\\
N\sin\varphi-P-T_{B}\cos\theta=0\ \ \ \ (2)
\end{array}\right. $$
Podemos isolar a $N$ na primeira equação e substituir na segunda para podermos explicitar $T_{B}$
$$T_{B}\frac{\sin\theta}{\cos\varphi}\sin\varphi-P-T_{B}\cos\theta=0$$
logo
$$T_{B}=\frac{P}{\left(\tan\varphi\sin\theta-\cos\theta\right)}\ \ \ \ (3)$$
Substituindo (3) em (1) obtemos
$$N=\frac{P\sin\theta}{\left(\sin\varphi\sin\theta-\cos\theta\cos\varphi\right)}$$
Dessa forma obtemos que as forças valem
$$\left\lbrace \begin{array}{lll}
T_A=mg\\
T_B=\frac{mg}{\left(\tan\varphi\sin\theta-\cos\theta\right)}\\
N=\frac{mg\sin\theta}{\left(\sin\varphi\sin\theta-\cos\theta\cos\varphi\right)}
\end{array}\right. $$
Escrevemos $\theta=\left( 90^\circ-\alpha\right) $ e dividimos as expressões por $g$ para obter o resultado em $kgf$
$$\left\lbrace \begin{array}{lll}
T_A=m\\
T_B=\frac{m}{\left(\tan\varphi\sin\left( 90^\circ-\alpha\right)-\cos\left( 90^\circ-\alpha\right)\right)}\\
N=\frac{m\sin\left( 90^\circ-\alpha\right)}{\left(\sin\varphi\sin\left( 90^\circ-\alpha\right)-\cos\left( 90^\circ-\alpha\right)\cos\varphi\right)}
\end{array}\right. $$
Sabemos que $\alpha=30^\circ$, $\varphi=45^\circ$ e $m=100kg$
$$\left\lbrace \begin{array}{lll}
T_A=100kgf\\
T_B= 273,2kgf\\
N=334,6kgf
\end{array}\right. $$



Comentários