O último dos sistemas básicos a ser estudado na introdução de circuitos é o circuito L-C. Diferente do circuito L-R, onde a energia magnética armazenada no indutor é dissipada por um resistor, o circuito L-C conserva sua energia, pois, a energia magnética no indutor é convertido em energia elétrica no capacitor e vice-versa. Semelhante ao que acontece em um sistema massa-mola a corrente no circuito L-C realiza um movimento oscilatório.
Para estudar esse sistema suponha um circuito organizado como na figura a baixo, quando a chave esta ligada a esquerda a fem $\varepsilon$ carrega o capacitor $C$ quando ele atingir sua carga máxima $Q_0$ a chave é virada para a direita, de forma que a fem não tem mais influência no sistema restando apenas os componente L-C. Note que nesse primeiro momento a energia total no sistema é $U_E=\frac{Q_0^2}{2C}$.
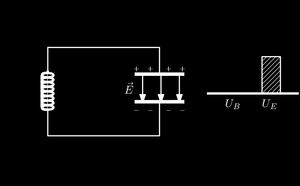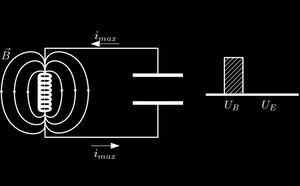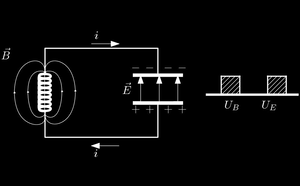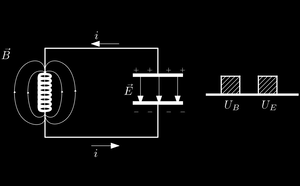
Depois de ser carregado o capacitor estabelece uma corrente que começa a carregar o indutor de modo que para um tempo $t$ qualquer é $U=U_E+U_L$, logo $$U=\frac{1}{2}\frac{q^2}{C}+\frac{1}{2}LI^2,\ \ \ \ (1)$$ onde $I$ é a corrente do sistema em um instante qualquer. Como a energia do sistema é conservada $\frac{dU}{dt}=0$, assim $$0=\frac{q}{C}\frac{dq}{dt}+LI\frac{dI}{dt}.$$ Lembrando que $I=\frac{dq}{dt}$, dessa forma teremos $$\frac{d^2q}{dt^2}+\frac{1}{LC}q=0\Rightarrow$$ $$\ddot{q}+\omega_0^2q=0.\ \ \ \ (2)$$ Onde $\omega_0=\frac{1}{\sqrt{LC}}$ é definido como frequência natural do sistema.
Podemos resolver essa equação diferencial supondo que a equação é da forma $q=e^{\lambda t}$, substituindo essa expressão na equação (2) obtemos $$\lambda^2e^{\lambda t}+\omega_0^2e^{\lambda t}=0\Rightarrow$$
$$\lambda^2+\omega_0^2=0$$ Os valores de $\lambda$ para essa equação são $\lambda_1=\omega_0 i$ e $\lambda_2=-\omega_0 i$, logo a solução geral dessa equação é $$q(t)=Ae^{\omega_0 i t}+Be^{-\omega_0 i t} \ \ \ \ (3)$$ Derivando essa expressão obtemos a corrente em função do tempo que é $$I(t)=\omega_0 i \left( Ae^{\omega_0 i t}-Be^{-\omega_0 i t}\right) .\ \ \ \ (4)$$ Note que as constantes a serem determinadas são $A$ e $B$. No momento em que o circuito é fechado a direita as condições iniciais são $Q(0)=Q_0$ e $I(0)=0$, substituindo esses valores nas equações (4) e (3) obtemos $$\left\lbrace \begin{array}{ll}
Q_0=A+B\ \ \ \ \ \ \ (5)\\
0=\omega_0 i \left( A-B\right)\ \ \ (6)
\end{array}\right.$$ Isolando $A$ em (5) e substituindo em (6) obtemos $B$, o mesmo vale para $B$. Dessa forma obtemos $$\left\lbrace \begin{array}{ll}
A=\frac{Q_0}{2}\\
B=\frac{Q_0}{2}
\end{array}\right.$$ Substituindo os valores de $A$ e $B$ em (3) obtemos $$
q(t)=Q_0\left( \frac{e^{\omega_0 i t}+e^{-\omega_0 i t}}{2}\right)
$$ Podemos usar a formula de Euler $e^{xi}=\cos(x)+i\sin(x)$ para reescrever essa expressão na forma trigonométrica $$
q(t)=Q_0\left( \frac{\cos(\omega_0 t)+i\sin(\omega_0 t)+\cos(-\omega_0 t)+i\sin(-\omega_0 t)}{2}\right)
\Rightarrow$$ $$
q(t)=Q_0\left( \frac{\cos(\omega_0 t)+i\sin(\omega_0 t)+\cos(\omega_0 t)-i\sin(\omega_0 t)}{2}\right)
\Rightarrow$$$$
q(t)=Q_0\left( \frac{2\cos\omega_0 t}{2}\right)
\Rightarrow$$ $$q(t)=Q_0\cos\omega_0 t, $$ que é a solução para a carga do sistema $L-C$, sendo a corrente sua derivada encontra-se que $$\left\lbrace \begin{array}{ll}
q(t)=Q_0\cos\omega_0 t\\
I(t)=-I_0\sin\omega_0 t
\end{array}\right.$$ Note que no gráfico a baixo mostra um movimento oscilatoriale das cargas no circuito.
Perceba que a corrente atinge seu valor mínimo quando a carga atinge seu valor máximo, isso condis com o fato de que a corrente cessa quando a energia não está em fluxo, isto é, totalmente na forma elétrica ou magnética. A energia magnética e elétrica variam no tempo de modo a deixar a energia toral $U$ constante. Como vimos na equação (1) a energia total do sistema é dada por
$$U=\frac{1}{2}\frac{q(t)^2}{C}+\frac{1}{2}LI(t)^2\Rightarrow$$
$$U=\frac{1}{2}\frac{Q_0^2}{C}\cos^2(\omega_0 t)+\frac{1}{2}LI_0^2\sin^2(\omega_0 t)$$
Note que $I_0^2=Q_0^2\omega_0^2=\frac{Q_0^2}{LC}$, logo
$$U=\frac{1}{2}\frac{Q_0^2}{C}\left( \cos^2\omega_0 t+\sin^2\omega_0 t\right) \Rightarrow$$
$$U=\frac{1}{2}\frac{Q_0^2}{C}$$
Note que, como esperado, essa é exatamente a energia inicialmente armazenada no capacitor.
Comentários