O circuito $R-L$ é formado por um gerador de potencial (fem), um resistor $R$ e um indutor $L$. Nessa situação estudaremos como o circuito se comporta quando a corrente produzida pela força eletromotriz (que pode ser uma bateria) é estacionária (constante no tempo). Suponha que o circuito esteja disposto como na figura a baixo.
Primeiro momento
Suponde que a chave $S_1$ esteja fechada no instante $t_0=0$ e tenhamos uma corrente nula $i(t_0)=0$, para $S_2$ aberta o circuito começa a ser percorrido pela corrente sendo nestas condições a malha efetiva dada pela figura abaixo.
Para calcular a corrente $i(t)$ em um instante de tempo qualquer podemos usar a lei das malhas (Kirchoff) e percorrer a malha no sentido horário para obter
$$\varepsilon-V_R-V_L=0$$
Onde $V_R$ é a queda de diferença de potencial devido ao resistor e $V_L$, como foi visto no estudo de
Auto-indutância e indutância mútua, é a queda de diferença de potencial do indutor, logo nossa equação é dada por $$\varepsilon-RI-L\frac{dI}{dt}=0.$$ Onde $I$ é a corrente. Essa é uma equação diferencial de primeira ordem de variáveis separáveis, logo podemos reescrever essa expressão como $$\frac{1}{\left( I-\frac{\varepsilon}{R}\right) }dI=-\frac{R}{L}dt.$$ No instante $t=0$ a corrente é $i(t_0)=0$ e para um momento posterior qualquer $i(t)=i$, logo $$\int_{0}^{i}\frac{1}{\left( I-\frac{\varepsilon}{R}\right) }dI=-\frac{R}{L}\int_{0}^{t}dt'.$$ Integrando essa expressão obtemos $$\left[ \ln\left| I-\frac{\varepsilon}{R}\right| \right]_{0}^{i}=-\frac{R}{L}t\Rightarrow$$
$$\ln\left| \frac{i-\frac{\varepsilon}{R}}{-\frac{\varepsilon}{R}}\right| =-\frac{R}{L}t\Rightarrow$$
$$\frac{\frac{\varepsilon}{R}-i}{\frac{\varepsilon}{R}} =e^{-\frac{R}{L}t}\Rightarrow$$
$$i(t) =\frac{\varepsilon}{R}\left( 1-e^{-\frac{R}{L}t}\right) $$ A corrente final é definida como $i_f=\frac{\varepsilon}{R}$ e $\tau_L=\frac{R}{L}$ é conhecida como constante de tempo indutiva, o que resulta na expressão
$$i(t) =i_f\left( 1-e^{-\frac{1}{\tau_L}t}\right). \ \ \ \ (1)$$
A corrente não é instantânea no circuito, para $t_0=0$ a corrente é nula e tem um caráter assintótico convergindo em $i_f=\frac{\varepsilon}{R}$ no infinito, a baixo está o gráfico da corrente em função do tempo.
A diferença de potencial $V_R=Ri$ entre os polos do resistor depende da corrente, logo também varia com o tempo. Usando a expressão (1) teremos $$V_R=Ri_f\left( 1-e^{-\frac{1}{\tau_L}t}\right)\Rightarrow$$
$$V_R=R\frac{\varepsilon}{R}\left( 1-e^{-\frac{1}{\tau_L}t}\right)\Rightarrow$$
$$V_R=\varepsilon\left( 1-e^{-\frac{1}{\tau_L}t}\right)z. \ \ \ \ (2)$$
O mesmo vale para diferença de potencial $V_L$ entre os polos do indutor que é dado por
$$V_L=L\frac{di}{dt}\Rightarrow$$
$$V_L=L\frac{d}{dt}\left[ i_f\left( 1-e^{-\frac{1}{\tau_L}t}\right)\right] \Rightarrow$$
$$V_L=Li_f\frac{1}{\tau_L}e^{-\frac{1}{\tau_L}t}\Rightarrow$$
$$V_L=L\frac{\varepsilon}{R}\frac{R}{L}e^{-\frac{1}{\tau_L}t}\Rightarrow$$
$$V_L=\varepsilon e^{-\frac{1}{\tau_L}t}. \ \ \ \ (3)$$
Com as equações (1) e (3) podemos interpretar a constante de tempo indutivo fazendo $t=\tau_L$ que resulta em $$\left\lbrace \begin{array}{ll}
V_L=\varepsilon e^{-1}\cong0,37\varepsilon\\
i =i_f\left( 1-e^{-1}\right)\cong0,63i_f
\end{array}\right. ,$$ dessa forma $\tau_L$ é o tempo que demora para a corrente atingir $63\%$ de seu valor máximo, da mesmo forma o tempo indutivo é o período que demora para a fem induzida do indutor atingir $37\%$ de seu valor final.
Segundo momento
Podemos agora estudar o que acontece quando a chave $S_2$ é fechada e a $S_1$ é aberta logo depois que a corrente atinge seu valor máximo. Com essa configuração a malha efetiva é a que está representada na figura abaixo.
Usando a lei de Kirchhoff percorremos novamente o circuito no sentido horário para obter $$RI+L\frac{dI}{dt}=0,$$ novamente essa é uma equação homogênea de primeiro gral de variáveis separáveis, e pode ser reescrita da seguinte forma $$\frac{1}{I}dI=-\frac{R}{L}dt.$$ No momento $t=0$ a corrente é $i_f$ e para um instante $t$ qualquer a corrente é $i$, logo $$\int_{i_f}^{i}\frac{1}{I}dI=-\frac{R}{L}\int_{0}^{t}dt',$$ o que resulta em $$\ln\left| \frac{i}{i_f}\right| =-\frac{R}{L}t,\Rightarrow$$ $$\frac{i}{i_f}=e^{-\frac{R}{L}t},\Rightarrow$$ $$i(t)=i_fe^{-\frac{R}{L}t},\Rightarrow$$ $$i(t)=i_fe^{-\frac{1}{\tau_L}t}.$$
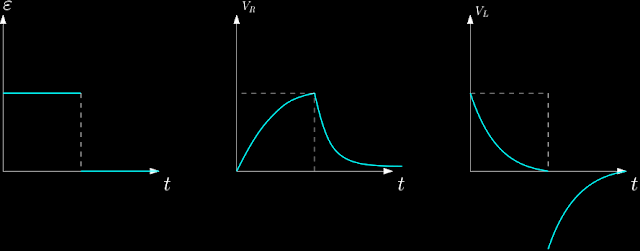
de forma análoga ao que fizemos no primeiro caso podemos encontrar a diferença de potencial entre os polos do resistor e do indutor, que são dados por
$$\left\lbrace \begin{array}{ll}
V_R=Ri_fe^{-\frac{1}{\tau_L}t}\\
V_L= -Ri_fe^{-\frac{1}{\tau_L}t}
\end{array}\right. $$
Note que a energia armazenada no indutor, como campo magnético, é convertida lentamente em energia térmica no condutor pelo efeito Jaule, por isso as diferenças de potencial entre o resistor e o indutor tem o mesmo valor, porém sinais opostos. A baixo estão representados os gráficos por partes do comportamento da diferença de potencial de cada componente do circuito.
Comentários