7.5) Considere uma espira circular de raio a
suspensa por um fio vertical $VV$ de constante
de torção $k$, situada num campo magnético $B$
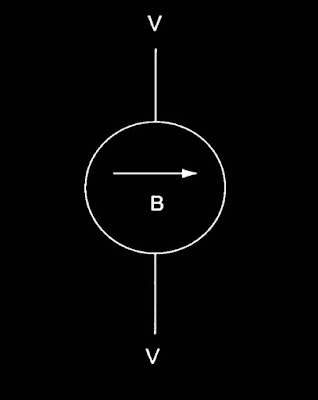
uniforme com a orientação inicial da figura.
O momento de inércia da espira em relação
ao eixo $VV$ é $I$. Faz-se passar através da espira um pulso rápido de corrente de duração
pira não tem tempo de se mover durante o
tempo. Mostre que o ângulo de deflexão máximo do plano da espira, $\theta_0$, é proporcional à carga total $q=it$ contida no pulso. Este é o princípio do galvanômetro balístico (em geral, se utiliza uma bobina com N esporas).
Na figura a baixo colocamos em perspectiva as forças e as grandezas que serão uteis na resolução.

Note que como existe uma corrente $i$ passando pela expira existem duas forças, $\vec{F}$ e $\vec{F}'$, de igual modulo e sentido oposto, estão agindo sobre a espira. a magnitude das forças é dada pela expressão
$$\left\lbrace \begin{array}{ll}
\vec{F}=id\vec{l}\times\vec{B}\\
\vec{F}'=id\vec{l}'\times\vec{B}
\end{array}\right. \Rightarrow\left\lbrace \begin{array}{ll}\vec{F}=idlB\hat{i}\times \hat{j}\\
\vec{F}'=-idlB\hat{i}\times \hat{j}
\end{array}\right.\Rightarrow \left\lbrace
\begin{array}{ll}
\vec{F}=idlB\hat{k}\\
\vec{F}'=-idlB\hat{k}
\end{array}\right. .$$
Embora as forças resultantes sejam nulas existe um torque não nulo durante a passagem da corrente dado por
$$\vec{\tau}=\vec{\tau}+\vec{\tau}'\Rightarrow$$
$$\vec{\tau}=\vec{F}\times\vec{a}+\vec{F}'\times\vec{a}'$$,
porém note que $\vec{a}'=-\vec{a}$ e $\vec{F}'=-\vec{F}$, logo o valor vetorial do torque é
$$\vec{\tau}=-2\vec{F}'\times\vec{a}'$$
Ou em modulo teremos
$$\tau=-2I\alpha\ \ \ \ \ (1)$$
Esse torque gera uma aceleração fazendo a espira adquirir uma frequência angular a partir do repouso, de forma que a expira foi de zero a $\omega$ em um intervalo angular $\theta_0$, logo
$$\omega^2=\omega_0^2+2\alpha\theta_0\Rightarrow$$
$$\omega^2=2\alpha\theta_0.\ \ \ \ (2)$$
Explicitando $\alpha$ em (1) e aplicando em (2) obtemos
$$\omega^2=-\frac{\tau}{I}\theta_0.\ \ \ \ (3)$$
Note que o torque, aplicado pela corrente $i$ na presença do campo $B$, torce a corda $VV$ que, de forma análoga ao caso de uma mola, tende a voltar para o estado inicial gerando um torque dado por
$$\tau=-k\theta_0.\ \ \ \ (4)$$
Isolando $\theta_0$ em (4) e aplicando em (3) obtemos
$$\omega^2=\frac{\tau^2}{kI}\Rightarrow$$
$$\omega=\frac{\tau}{\sqrt{kI}}\Rightarrow$$
$$\frac{d\theta}{dt}=\frac{\tau}{\sqrt{kI}}\Rightarrow$$
$$d\theta=\frac{\tau}{\sqrt{kI}}dt\Rightarrow$$
$$\int_0^{\theta_0} d\theta=\int_0^t\frac{\tau}{\sqrt{kI}}dt\Rightarrow$$
$$\theta_0=\frac{\tau}{\sqrt{kI}}t,\ \ \ \ \ (5)$$ por outro lado o torque também pode ser expresso em termos do momento de dipolo
$$\vec{\tau}=\vec{m}\times\vec{B}\Rightarrow$$
$$\tau=mB\sin90°\Rightarrow$$
$$\tau=mB\ \ \ \ (6)$$
Aplicando a expressão (6) na equação (5) obtemos
$$\theta_0=\frac{mB}{\sqrt{kI}}t$$
O momento de inércia é a área $A$ delimitada pela expira circular multiplicado pela corrente $i$, isto é, $m=iA=i\pi a^2$ logo
$$\theta_0=\frac{(it)\pi a^2B}{\sqrt{kI}}\Rightarrow$$
$$\theta_0=\frac{q\pi a^2B}{\sqrt{kI}}$$



Comentários