8.3) Uma espira em forma de retângulo, de lados $2a$ e $2b$, transporta uma corrente de intensidade $i$. (a) Calcule a magnitude do campo magnético no centro do retângulo. (b) Tome o limite do resultado para $a>>b$ e discuta a relação com o encontro no problema 2.
a) Podemos usar a lei de Biot-Savart para determinar o campo da espira, basta calcular o campo para dois lados diferente e dobrar o resultado, pois fios retilineos de comprimento $2a$ ou $2b$ contribuem com a mesma intensidade para o campo.
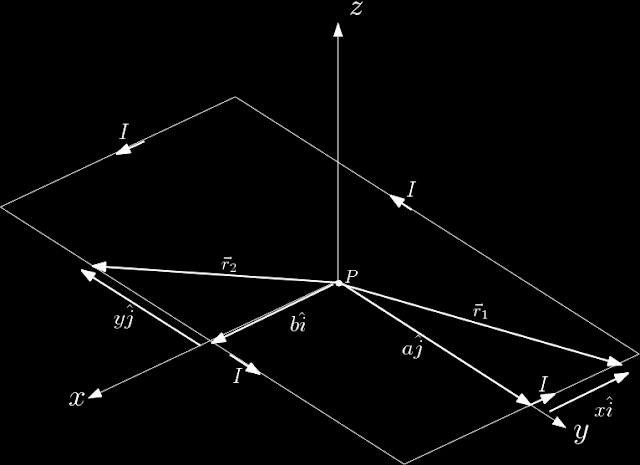
Como na figura a posição $\vec{r}_1$ e $\vec{r}_2$ das espiras são dadas por
$$\left\lbrace \begin{array}{ll}
\vec{r}_1=x\hat{i}+a\hat{j}\\
\vec{r}_2=b\hat{i}+y\hat{j}
\end{array}\right. $$
o vetor simétrico, que aponta do elemento de corrente até a origem é
$$\left\lbrace \begin{array}{ll}
\vec{r'}_1=-x\hat{i}-a\hat{j}\\
\vec{r'}_2=-b\hat{i}-y\hat{j}
\end{array}\right. $$
Portanto o campo é da forma
$$\vec{B}=2\vec{B}_1+2\vec{B}_2$$
Pela lei de Biot-Savart temos que
$$\vec{B}=2\frac{\mu_0i}{4\pi}\int_{b}^{-b}\frac{d\vec{l}\times\vec{r'}_1}{r'^3_1}+2\frac{\mu_0i}{4\pi}\int_{-a}^{a}\frac{d\vec{l}\times\vec{r'}_2}{r'^3_2}\Rightarrow$$
$$\vec{B}=\frac{\mu_0i}{2\pi}\int_{b}^{-b}\frac{dx\hat{i}\times(-x\hat{i}-a\hat{j})}{[a^2+x^2]^{\frac{3}{2}}}+\frac{\mu_0i}{2\pi}\int_{-a}^{a}\frac{dy\hat{j}\times(-b\hat{i}-y\hat{j})}{[b^2+y^2]^{\frac{3}{2}}}\Rightarrow$$
$$\vec{B}=\frac{\mu_0i}{2\pi}\int_{b}^{-b}\frac{-x\hat{i}\times\hat{i}-a\hat{i}\times\hat{j}}{[a^2+x^2]^{\frac{3}{2}}}dx+\frac{\mu_0i}{2\pi}\int_{-a}^{a}\frac{-b\hat{j}\times\hat{i}-y\hat{j}\times\hat{j}}{[b^2+y^2]^{\frac{3}{2}}}dy$$
Os seguintes produtos vetoriais $\hat{i}\times\hat{i}$ e $\hat{j}\times\hat{j}$ são nulos, enquanto $\hat{i}\times\hat{j}=\hat{k}$ e $\hat{j}\times\hat{i}=-\hat{k}$, o que resulta em
$$\vec{B}=-\frac{\mu_0i}{2\pi}\int_{b}^{-b}\frac{a}{[a^2+x^2]^{\frac{3}{2}}}dx\hat{k}+\frac{\mu_0i}{2\pi}\int_{-a}^{a}\frac{b}{[b^2+y^2]^{\frac{3}{2}}}dy\hat{k}$$
Realizando a substituição $x=a\tan\theta$ no primeiro termo e $y=b\tan\theta$ no segundo termo obtemos
$$\vec{B}=-\frac{\mu_0i}{2\pi a}\int\cos\theta d\theta\hat{k}+\frac{\mu_0i}{2\pi b}\int \cos\theta d\theta\hat{k}\Rightarrow$$
$$\vec{B}=-\frac{\mu_0i}{2\pi a}\left[ \sin\theta\right]_\theta\hat{k}+\frac{\mu_0i}{2\pi b}\left[ \sin\theta\right]_\theta \hat{k}$$
Devemos agora voltar para as variáveis $x$ e $y$, para fazer isso basta lembrar que
$$\begin{array}{ll}
\tan\theta=\frac{x}{a}\Rightarrow 1+\tan^2\theta=1+\frac{x^2}{a^2}\Rightarrow\sec^2\theta=\frac{a^2+x^2}{a^2}\Rightarrow\cos^2\theta=\frac{a^2}{a^2+x^2}\Rightarrow\sin\theta=\frac{x}{(a^2+x^2)^{\frac{1}{2}}}\\
\tan\theta=\frac{y}{b}\Rightarrow 1+\tan^2\theta=1+\frac{y^2}{b^2}\Rightarrow\sec^2\theta=\frac{b^2+y^2}{b^2}\Rightarrow\cos^2\theta=\frac{b^2}{b^2+y^2}\Rightarrow\sin\theta=\frac{y}{(b^2+y^2)^{\frac{1}{2}}}
\end{array}$$
Logo
$$\vec{B}=-\frac{\mu_0i}{2\pi a}\left[ \frac{x}{(a^2+x^2)^{\frac{1}{2}}}\right]_b^{-b}\hat{k}+\frac{\mu_0i}{2\pi b}\left[ \frac{y}{(b^2+y^2)^{\frac{1}{2}}}\right]_{-a}^a \hat{k}\Rightarrow$$
$$\vec{B}=-\frac{\mu_0i}{2\pi a}\left[ -\frac{b}{(a^2+b^2)^{\frac{1}{2}}}-\frac{b}{(a^2+b^2)^{\frac{1}{2}}}\right]\hat{k}+\frac{\mu_0i}{2\pi b}\left[ \frac{a}{(b^2+a^2)^{\frac{1}{2}}}+\frac{a}{(b^2+a^2)^{\frac{1}{2}}}\right] \hat{k}\Rightarrow$$
$$\vec{B}=\frac{\mu_0i}{\pi }\frac{1}{(a^2+b^2)^{\frac{1}{2}}}\left[\frac{b^2+a^2}{ab}\right]\hat{k}\Rightarrow$$
$$\vec{B}=\frac{\mu_0i}{\pi ab }(a^2+b^2)^{\frac{1}{2}}\hat{k}$$
b) Supondo que $a>>b$ teremos
$$\vec{B}=\frac{\mu_0i}{\pi b }\hat{k}$$
Como na questão anterior o campo é descontinuo na região próximo do condutor.



Comentários