8.1) No modelo de Bohr para o átomo de hidrogênio, o raio $a_0$ da 1° órbita circular do elétron é dado pela condição de quantização $L=\hbar$, onde $\hbar=1.055\times10^{-34}J.s$ e $L$ é a magnitude do momento angular do elétron em relação ao núcleo (próton). (a) Usando essa condição, mostre que $a_0=4\pi\varepsilon_0\hbar^2/(me^2)$, onde $m$ e $e$ são as magnitudes da massa e carga do elétron, respectivamente. Calcule o valor de $a_0$. (b) Calcule a intensidade de corrente $i$ associada ao movimento do elétron na sua órbita. (c) Calcule a magnitude do campo magnético produzido por essa corrente na posição do núcleo. (d) Calcule a magnitude $\mu_B$ do momento de dipolo magnético associado á corrente (magneton de Bohr), e mostre que $\mu_B/L=e/(2m)$ (razão giromagnética clássica) Obtenha o valor numérico de $\mu_B$.
a) A força que mantêm o elétron em órbita é devido à força $\vec{F}_e$ de atração entre o elétron e o próton.
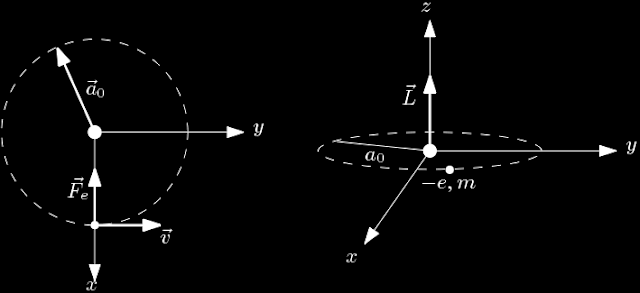
Em modulo tal força elétrica é dada por
$$F_e=-\frac{1}{4\pi \varepsilon_0}\frac{e^2}{a_0^2}.$$
Nesse caso a força magnética é também uma força centrípeta dada por $F_e=-m\frac{v^2}{a_0}$, logo
$$m\frac{v^2}{a_0}=\frac{1}{4\pi \varepsilon_0}\frac{e^2}{a_0^2}\Rightarrow$$
$$a_0v^2=\frac{1}{4\pi \varepsilon_0}\frac{e^2}{m}.$$
A velocidade pode ser reescrita da seguinte forma $v=a_0\omega$ o que resulta em
$$a_0^3\omega^2=\frac{1}{4\pi \varepsilon_0}\frac{e^2}{m}.$$
O momento angular $L$ em relação ao núcleo é dado por $L=ma_0^2\omega$, explicitando $\omega$ obtemos $\omega=\frac{L}{ma_0^2}$ o que nos dá
$$a_0^3\frac{L^2}{m^2a_0^4}=\frac{1}{4\pi \varepsilon_0}\frac{e^2}{m}.\Rightarrow$$
$$\frac{L^2}{a_0}=\frac{me^2}{4\pi \varepsilon_0}\Rightarrow$$
$$\frac{1}{a_0}=\frac{me^2}{4L^2\pi \varepsilon_0}\Rightarrow$$
$$a_0=\frac{4\pi \varepsilon_0}{me^2}L^2$$
Devido à hipótese de quantização $L=\hbar$, finalmente obtemos
$$a_0=\frac{4\pi \varepsilon_0}{me^2}\hbar^2\ \ \ \ (1)$$
todos os valores na equação (1) são conhecidos
$$a_0=\frac{4(3,14)(8,8\times10^{-12}C^2/N^2.m^2)}{(9,1\times10^{-31} kg)(1,6\times10^{-19} C)^2}(1,055\times10^{-34}J.s)^2=0,5\times10^{-10}m= 0,5\ Angstrom$$
Dessa forma o raio atômico de Bohr é $a_0=0,5\ Angstrom$
b) A corrente $i$ é dada pela variação da carga no tempo, que nesse caso é dado simplesmente pela carga do elétron sobre o seu período,
$$i=\frac{dq}{dt}=\frac{e}{T}=e\frac{1}{T}.$$
Note que no termo aparece a expressão $1/T$ que nada mais é do que a frequência $f=\frac{1}{T}=\frac{\omega}{2\pi}$, logo
$$i=e\frac{\omega}{2\pi}$$
O momento angular nos da a expressão para $\omega$, pois, $L=ma_0^2\omega$ e pela hipótese de quantização obtemos que $\omega=\frac{\hbar}{ma_0^2}$, desse modo
$$i=\frac{e\hbar}{2\pi ma_0^2}\ \ \ \ (2)$$
Todos os valores de (2) são conhecidos de modo que
$$i=\frac{(1,6\times10^{-19} C)(1,055\times10^{-34}J.s)}{2(3,14)(9,1\times10^{-31} kg)(0,5\times10^{-10})^2m}=1,05\times10^{-3}A$$
c) Usando a lei de Biot e Savart para determinar o campo $\vec{B}$, que nesse caso é dado por
$$\vec{B}=\frac{\mu_0 i}{4\pi}\int \frac{d\vec{l}\times\vec{a_0}}{a_0^3}$$
Como $d\vec{l}\times\vec{a_0}=dla_0\sin(\frac{\pi}{2})=dla_0$ obtemos o campo em modulo
$$B=\frac{\mu_0 i}{4\pi a_0^2}\int dl$$
O elemento de comprimento $dl$ é um pequeno pedaço da trajetória do elétron que nesse caso é um círculo de raio $a_0$, logo obtemos
$$B=\frac{\mu_0 i}{4\pi a_0^2}2\pi a_0$$
portanto
$$B=\frac{\mu_0 i}{2a_0}\ \ \ \ (3)$$
Todos esses valores são conhecidos
$$B=\frac{(4(3,14)\times10^{-7} N/A^2)(1,05\times10^{-3}A)}{2(0,5\times10^{-10}m)}=12,5T$$
d) O momento de dipolo magnético é dado por $m=iA$, onde $A$ é a área delimitada pelo circuito, podemos pensar na trajetória do elétron como um circuito elétrico de modo que $A=\pi a_0^2$, desse modo o magneton de Bohr $\mu_B=m$ é dada por
$$\mu_B=i\pi a_0^2$$
Aplicando a expressão da corrente associada ao giro do elétron, dada pela equação (2), obtemos
$$\mu_B=\frac{e\hbar}{2\pi ma_0^2}\pi a_0^2\Rightarrow$$
$$\mu_B=\frac{e\hbar}{2m}$$
O que tem valor numérico dado por $\mu_B=9,3\times10^{-24}A.m^2$. Por fim podemos obter a razão giromagnética clássica, usando a hipótese de quantização no magneton de Bohr, para obter
$$\mu_B=\frac{eL}{2m}\Rightarrow$$
$$\frac{\mu_B}{L}=\frac{e}{2m}$$



Comentários