Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 13.7

13.7) Considere um balde cilíndrico com água, em rotação com velocidade angular $\omega$ em torno de um eixo vertical, após atingida a situação de equilíbrio, em que a água está girando juntamente com o balde [seç.13.7]. Para obter a forma da superfície de equilíbrio da água, utilize o fato de que o fluido em equilíbrio não pode suportar forças tangenciais a sua superfície, de modo que, no referencial do balde, as forças atuantes na superfície tem de ser normal a ela. Prove que a superfície do balde é um paraboloide de revolução, achando sua equação no sistema de coordenadas com origem no ponto em que a superfície corta o eixo de rotação $oz$.  

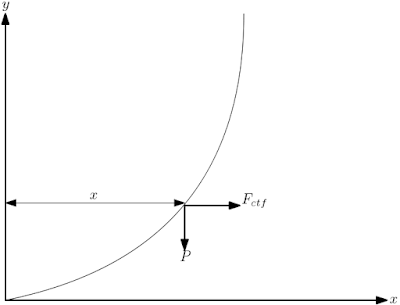
Podemos adotar o sistema de referencial com eixo $oy$ sobre o eixo de rotação, e desenha a suposta superfície nesse referencial, uma partícula de água com massa $m$ a uma distância $x$ do eixo de rotação e sobre essa superfície está sujeita ao efeito de duas forças, a força peso $P$ e a força centrifuga $F_{ctf}$,

Podemos então pensar que a reta tangente a superfície nesse ponto faz um ângulo $\theta$ com a horizontal de modo que a tangente desse ângulo é a derivada da curva de revolução,

Adotando um referencial linha com eixo $oy'$ sobre a reta tangente a esse ponto,

Note que podemos decompor as forças que atuam sobre a massa de água $m$ em relação ao referencial com linha de modo a representar a situação de equilíbrio da mesma, $$\left\lbrace \begin{array}{ll} F_{ctf}\sin\theta+P\cos\theta=0\\ F_{ctf}\cos\theta-P\sin\theta=0\\ \end{array}\right. $$ Da segunda equação encontramos a seguinte relação $$\tan\theta=\frac{F_{ctf}}{P}$$ Que é a derivada da curva no referencial sem linha, ou seja, $$\frac{dy}{dx}=\frac{\omega^2x}{g}$$ Integrando a expressão em relação a $x$ obtemos, $$y=\frac{\omega^2}{2g}x^2+C$$ Como a condição inicial é $y(0)=0$ teremos que $C=0$, $$y=\frac{\omega^2}{2g}x^2$$ A curva de revolução é claramente uma parábola, o que implica que a superfície é uma paraboloide centrado na origem com concavidade positiva.