Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 9.8

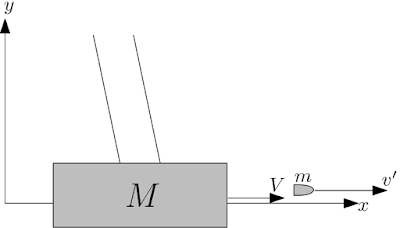
9,8) Uma bala de $5 g$ incide sobre um pêndulo balístico de massa igual a 2 kg, com uma velocidade de $400 m/s$, atravessa-o e emerge do outro lado com uma velocidade de $100 m/s$. Calcule a altura de elevação do pêndulo, desprezando a elevação durante o tempo que a bala leva para atravessá-lo. Verifique a validade desta aproximação. 

 Vamos supor inicialmente que o tempo que a bala permanece destro do pendulo balístico pode ser desprezada, de tal forma que a bala transfira momento para o pendulo de forma instantânea por meio de uma colisão elástica.

Supondo que a bala de massa $m$ inicialmente a uma velocidade $v$ transfira parte de seu momento para o pendulo balístico de massa $M$ de modo que logo após a bala emergir do pendulo ela desacelere para uma velocidade $v'$ enquanto o pendulo adquire uma velocidade $V$, supondo que a troca de momento seja dada de forma perfeitamente elástica podemos supor que o momento é conservado, logo o momento inicial é equivalente ao final, $$mv=MV+mv'\Rightarrow$$ $$V=\frac{m}{M}(v-v')$$ Apos ganhar essa energia cinética, o pendulo começará a transformar tal energia cinética em potencial gravitacional, estamos supondo que a energia mecânica do pendulo é conservada,

dessa forma por conservação de energia teremos que, $$\frac{1}{2}MV^2=Mgh\Rightarrow$$ $$\frac{1}{2}\left( \frac{m}{M}(v-v')\right) ^2=gh\Rightarrow$$ $$h=\frac{1}{2}\frac{m^2}{gM^2}\left( v-v'\right)^2$$ Ao fazer as devidas conversões de unidade de medida para o sistema SI e aplicar os valores na equação assina obteremos o valor, $$h=0,028m$$ De fato esse tempo em que a bala fica dentro do pendulo é desprezível. Supondo a velocidade media da bala dentro do pendulo como $v_m=300m/s$ supondo que o pendulo tenha um comprimento $d$ o tempo médio $\Delta t$ que a bala permanece no pendulo será, $$\Delta t=\frac{d}{300}$$ se que o pendulo tenha $d=1m$ na pior das hipóteses teremos, $$\Delta t=0,003s$$