Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 9.5

9.5) Uma partícula de massa m desloca-se com velocidade v em direção a duas outras idênticas, de alinhadas com ela, inicialmente separadas e em repouso (veja fig.). As colisões entre as partículas são todas elásticas. (a) Mostre que, para $m_1 \leqslant m_2$ haverá duas colisões, e calcule as velocidades finais das três partículas. (b) Mostre que, para $m_1>m_2$, haverá três colisões, e calcule as velocidades finais das três partículas. (c) Verifique que, no caso (a), o resultado para a primeira e a terceira partícula é o mesmo que se a partícula intermediária não existisse. 

 a) Para uma colisão elástica em uma dimensão de forma geral podemos utilizar as seguintes equações que foram deduzidas no livro, $$\left\lbrace \begin{array}{ll} v_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}+ \left( \frac{2m_2}{m_1+m_2}\right)v_{2i}\\ v_{2f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}-\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{2i}\\ \end{array}\right.$$ Na primeira colisão teremos a seguinte situação,

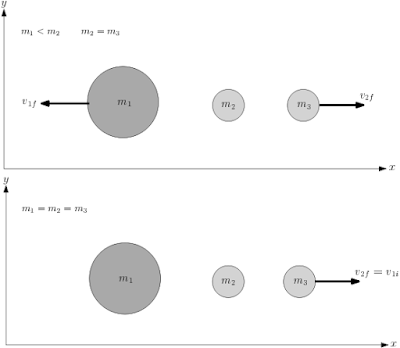
Supondo que $v_{2i}=0$ a velocidade da massa $m_2$ no instante antes a colisão, teremos as velocidades, $$\left\lbrace \begin{array}{ll} v_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ v_{2f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ Note que devemos discutir o sinal da subtração da primeira equação, como, por hipótese, $m_1\leqslant m_2$ então a massa $m_1$ ficara em repouso caso $m_1=m_2$ ou voltara no sentido oposto ao sentido inicial com velocidade dada pela primeira equação,

A massa $m_2$ continua se dirigindo com velocidade $v_{2f}$ na direção da massa $m_3$, supondo que $m_3$ estava em repouso em um momento inicial teremos as seguintes velocidades resultantes da colisão, $$\left\lbrace \begin{array}{ll} v'_{2f}=\left( \frac{m_2-m_3}{m_2+m_3}\right)v_{2f}=\left( \frac{m_2-m_3}{m_2+m_3}\right)\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ v_{3f}=\left( \frac{2m_2}{m_2+m_3}\right)v_{2f}=\left( \frac{2m_2}{m_2+m_3}\right)\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ Note que como a hipótese posterior é de que $m_3=m_2$, $$\left\lbrace \begin{array}{ll} v'_{2f}=0\\ v_{3f}=v_{2f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ Então a massa $m_2$ ficara parada após a segunda colisão de forma que o momento de $m_2$ é completamente transferido para a massa $m_3$, adquirindo assim uma velocidade $v_{2f}$, perceba ainda que como no primeiro caso a massa $m_1$ ou ficou parada, ou reverteu o sentido de seu movimento não ocorre risco de acontecer uma terceira colisão, de forma que as situações possíveis para o movimento final do sistema são as seguintes,

$$\left\lbrace \begin{array}{lll} v'_{2f}=0\\ v_{3f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ v_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ b) Supondo que $m_1>m_2$ e considerando que $m_2$ estava parado no momento inicial, as velocidades finais segundo as equações propostas inicialmente serão, $$\left\lbrace \begin{array}{ll} v_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ v_{2f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ Note que o sinal da primeira equação é positiva, pois, $m_1>m_2$, ou seja, $m_1$ e $m_2$ viajam em direção da massa $m_3$ com velocidades dadas pelas equações acima,

Após a massa $m_2$ colidir com $m_3$ ela ficará em repouso, enquanto o momento de $m_2$ será totalmente transferido para $m_3$ acelerando-a para uma velocidade $v_{2f}$,

Basta agora calcular as velocidades finais de $m_2$ e $m_3$ na terceira colisão, $$\left\lbrace \begin{array}{ll} v'_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ v'_{2f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1f}=\left( \frac{2m_1}{m_1+m_2}\right)\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ A situação final do sistema será então,

$$\left\lbrace \begin{array}{lll} v'_{1f}=\left( \frac{m_1-m_2}{m_1+m_2}\right)\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ v'_{2f}=\left( \frac{2m_1}{m_1+m_2}\right)\left( \frac{m_1-m_2}{m_1+m_2}\right)v_{1i}\\ v_{3f}=\left( \frac{2m_1}{m_1+m_2}\right)v_{1i}\\ \end{array}\right.$$ c) De fato, supondo que a segunda partícula não exista então as velocidades finais serão, $$\left\lbrace \begin{array}{ll} v_{1f}=\frac{m_1-m_3}{m_1+m_3}v_{1i}\\ v_{3f}=\frac{2m_1}{m_1+m_3}v_{1i}\\ \end{array}\right.$$ Fazendo $m_3=m_2$ obtemos, $$\left\lbrace \begin{array}{ll} v_{1f}=\frac{m_1-m_2}{m_1+m_2}v_{1i}\\ v_{3f}=\frac{2m_1}{m_1+m_2}v_{1i}\\ \end{array}\right.$$