Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 9.3

9.3) Considere a colisão elástica entre duas partículas de massas $m_1$ e $m_2$ que se movem em uma dimensão. (a) Verifique, a partir das (9.4.11), que a velocidade do $CM$ se conserva na colisão. (b) Calcule as velocidades iniciais $v_{1i}$ e $v′_{2i}$ das duas partículas em relação ao $CM$ do sistema, exprimindo-as em função da velocidade relativa inicial $v_{ri}$ da partícula 2 em relação à partícula 1 e da massa total $M=m_1+m_2$ . Qual é a relação entre $v′_{ri}$ e $v_{ri}$ ? (c) Faça o mesmo para as velocidades finais $v′_{1f}$ e $v′_{2f}$ em relação ao CM, com auxilio das (9.4.11). Qual é a relação entre $v′_{rf}$ e $v_{rf}$ (a velocidade relativa final)? E entre $v′_{rf}$ e $v′_{ri}$ ? (d) Interprete os resultados de (a) a (c), descrevendo como ocorre a colisão vista do referencial do $CM$. 

 a) Como o centro de massa está se movendo em relação a um referencial parado em segundo $m_1$ e $m_2$, o centro de massa tem uma velocidade $V_i$, logo, dizer que o centro de massa é conservado após a colisão entre as duas partículas é dizer que depois da colisão o centro de massa tem uma velocidade $V_f$ tal que $v_i=V_f$. O livro nos da uma demostração na sessão 9.5 de que as velocidades finais, $v_{f1}$ e $v_{f2}$, de duas, $m_1$ e $m_2$, partículas que colidem frontalmente em uma dimensão podem ser escritas de forma geral em função das velocidades iniciais, $v_{i1}$ e $v_{i1}$, $$\left\lbrace \begin{array}{ll} v_{f_1}=\frac{m_1-m_2}{m_1+m_2}v_{i1}+\frac{2m_2}{m_1+m_2}v_{i2}\ \ \ (1)\\ v_{f_2}=\frac{2m_1}{m_1+m_2}v_{i1}-\frac{m_1-m_2}{m_1+m_2}v_{i2}\ \ \ (2)\\ \end{array}\right.$$ Como é uma colisão elástica estamos supondo que o momento foi conservado no processo, isso é, $P_i=P_f$, então intuitivamente devemos multiplicar as expressões das velocidades finais pelas suas respectivas massa de forma que encontramos agora as expressões do momento final de cada partícula, $$\left\lbrace \begin{array}{ll} m_1v_{f_1}=m_1\frac{m_1-m_2}{m_1+m_2}v_{i1}+m_1\frac{2m_2}{m_1+m_2}v_{i2}\\ m_2v_{f_2}=m_2\frac{2m_1}{m_1+m_2}v_{i1}-m_2\frac{m_1-m_2}{m_1+m_2}v_{i2}\\ \end{array}\right.$$ Somando as duas equações obtemos o momento total final $P_f=P_{1f}+P_{2f}=m_1v_{f1}+m_2v_{f2}$, logo, $$m_2v_{f_2}+m_2v_{f_2}=m_1\frac{m_1-m_2}{m_1+m_2}v_{i1}+m_1\frac{2m_2}{m_1+m_2}v_{i2}+m_2\frac{2m_1}{m_1+m_2}v_{i1}-m_2\frac{m_1-m_2}{m_1+m_2}v_{i2}$$ Reorganizando a equação obtemos, $$m_2v_{f_2}+m_2v_{f_2}=\frac{m^2_1v_{i1}-m_1m_2v_{i1}+2m_2m_1v_{i2}+2m_2m_1v_{i1}-m_2m_1v_{i2}+m^2_2v_{i2}}{m_1+m_2}\Rightarrow$$ $$m_2v_{f_2}+m_2v_{f_2}=\frac{\left( m_1+m_2\right)m_1v_{i1} +\left( m_1+m_2\right)m_2v_{i2} }{m_1+m_2}\Rightarrow$$ $$\frac{m_2v_{f_2}+m_2v_{f_2}}{m_1+m_2}=\frac{\left( m_1+m_2\right)m_1v_{i1} +\left( m_1+m_2\right)m_2v_{i2} }{\left( m_1+m_2\right)^2 }\Rightarrow$$ $$V_f=\frac{m_2v_{f_2}+m_2v_{f_2}}{m_1+m_2}=\frac{m_1v_{i1} +m_2v_{i2} }{ m_1+m_2 }=V_i$$ Note que as expressões do lado esquerdo e direito nada mais são do que as velocidades do centro de massa $V_f$ e $V_i$ respectivamente, logo, $$V_f=V_i$$ Como queríamos demostrar. b) Queremos agora descobrir qual é a velocidade inicial, $v'_i1$ e $v'_i2$ , das partículas $m_1$ e $m_2$ se colocarmos o referencial se movendo sobre o centro de massa $CM$ das duas partículas,

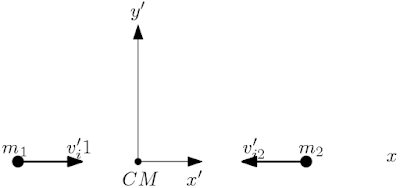
Olhando para as partículas no referencial linha do centro de massa é isso o que vemos,

Podemos descobrir essa velocidade usando a transformação de Galileu, a velocidade no referencial sem linha é igual a sola da velocidade do referencial com linha com a partícula no referencial com linha, ou seja, $$\left\lbrace \begin{array}{ll} v_{i1}=v'_{i1}+V_i\\ v_{i2}=v'_{i2}+V_i\\ \end{array}\right.$$ Logo a velocidade no referencial com linha será dada por, $$\left\lbrace \begin{array}{ll} v'_{i1}=v_{i1}-V_i\ \ \ (3)\\ v'_{i2}=v_{i2}-V_i\ \ \ (4)\\ \end{array}\right.$$ Vamos abrir a expressão evidenciando as partes de $V_i$, $$\left\lbrace \begin{array}{ll} v'_{i1}=v_{i1}-\frac{m_1v_{i1}+m_2v_{i2}}{m_1+m_2}\\ v'_{i2}=v_{i2}-\frac{m_1v_{i1}+m_2v_{i2}}{m_1+m_2}\\ \end{array}\right.$$ Reorganizando a expressão teremos, $$\left\lbrace \begin{array}{ll} v'_{i1}=\frac{m_1v_{i1}+m_2v_{i1}-m_1v_{i1}-m_2v_{i2}}{m_1+m_2}\\ v'_{i2}=\frac{m_1v_{i2}+m_2v_{i2}-m_1v_{i1}-m_2v_{i2}}{m_1+m_2}\\ \end{array}\right. \Rightarrow$$ $$\left\lbrace \begin{array}{ll} v'_{i1}=-\frac{m_2}{m_1+m_2}\left( v_{i2}-v_{i1}\right) \\ v'_{i2}=\frac{m_1}{m_1+m_2}\left( v_{i2}-v_{i1}\right) \\ \end{array}\right.$$ Note que a velocidade relativa $v_{ri}$ da partícula 2 em relação a partícula 1 é $v_{ri}=v_{i2}-v_{i1}$, assim como podemos escrever a massa total do sistema com $M=m_1+m_2$, $$\left\lbrace \begin{array}{ll} v'_{i1}=-\frac{m_2}{M}v_{ri}\\ v'_{i2}=\frac{m_1}{M}v_{ri}\\ \end{array}\right.$$ Podemos por fim relacionar as velocidades relativas da partícula 2 em relação a partícula 1 no referencial sem linha $v_{ri}$ e com a partícula no referencial com linha $v'_{ri}$ lembrando que $v_{ri}=v_{i2}-v_{i1}$ e que a mesma relação de velocidade relativa da partícula 2 em relação a 1 vale para o referencial com linha, $$v'_{ri}=v'_{i2}-v'_{i1}$$ Usando as equações (3) e (4) obtemos, $$v'_{ri}=\left( v_{i2}-V_i\right) -\left( v_{i1}-V_i\right)$$ Isto é, $$v'_{ri}=v_{i2}-v_{i1}$$ Que nada mais é que, $$v'_{ri}=v_{ri}$$ c) Da mesma forma que na letra b) encontramos as velocidades iniciais de $m_1$ e $m_2$ antes da colisão no referencial do centro de massa, referencial com linha, podemos fazer a mesma coisa para as velocidade $v_{f1}$ e $v_{f2}$ usando como auxilio as equações (1) e (2), mas primeiro,

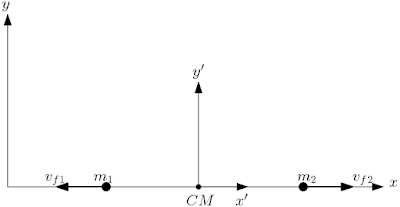
Ou olhando da perspectiva do centro de massa,

Note que nessa nova situação as velocidades foram invertidas de sentido, usando novamente a transformação de galileu obtemos, $$\left\lbrace \begin{array}{ll} v_{f1}=v'_{f1}+V_f\\ v_{f2}=v'_{f2}+V_f\\ \end{array}\right.$$ Lembrando que $V_i=V_f$ obtemos, $$\left\lbrace \begin{array}{ll} v'_{f1}=v_{f1}-V_i\ \ \ (5)\\ v'_{f2}=v_{f2}-V_i\ \ \ (6)\\ \end{array}\right.$$ Abrindo a expressão de $V_i$, $v_{f1}$ e $v_{f2}$ obtemos, $$\left\lbrace \begin{array}{ll} v'_{f1}=\frac{m_1-m_2}{m_1+m_2}v_{i1}+\frac{2m_2}{m_1+m_2}v_{i2}-\frac{m_1v_{i1}+m_2v_{i2}}{m_1+m_2}\\ v'_{f2}=\frac{2m_1}{m_1+m_2}v_{i1}-\frac{m_1-m_2}{m_1+m_2}v_{i2}-\frac{m_1v_{i1}+m_2v_{i2}}{m_1+m_2}\\ \end{array}\right.$$ Reorganizando os termos de modo a formar apenas uma parcela, $$\left\lbrace \begin{array}{ll} v'_{f1}=\frac{m_2}{m_1+m_2}\left(v_{i2}-v_{i1}\right) \\ v'_{f2}=-\frac{m_1}{m_1+m_2}\left(v_{i2}-v_{i1}\right) \\ \end{array}\right.$$ Usando novamente a redução $v_{ri}$ e $M$ $$\left\lbrace \begin{array}{ll} v'_{f1}=\frac{m_2}{M}v_{ri}=-v'_{i1}\\ v'_{f2}=-\frac{m_1}{M}v_{ri}=-v'_{i2}\\ \end{array}\right.$$ Usando a relação, $$v'_{rf}=v'_{f2}-v'_{f1}$$ Podemos obter outra relação interessante, usando as equações (5) e (6) obtemos $$v'_{rf}=\left( v_{f2}-V_i\right) -\left( v_{f1}-V_i\right) \Rightarrow$$ $$v'_{rf}=v_{f2}-v_{f1}\Rightarrow$$ $$v'_{rf}=v_{rf}$$ Porém olhando do referencial com linha, referencial do centro de massa, sabermos que as velocidades se invertem, ou seja $v'_{ri}=-v'_{rf}$, logo, $$v'_{rf}=-v'_{ri}$$ d) Olhando do referencial com linha, ou seja, do referencial do centro de massa, veríamos as partículas se aproximar da origem com velocidade inicial igual e sentido oposto, assim como veríamos elas se afastar com velocidade final igual e sentido oposto.