Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 9.1

9.1) Calcule a magnitude (em $kgf$) da força impulsiva que atua em cada um dos exemplos seguintes: (a) Num saque de jogo de tênis, a bola, de massa igual a $60g$, é lançada com uma velocidade de $40m/s$; o tempo de contato com a raquete é da ordem de $0,005s$ (b) Um jogador de futebol cobra um pênalti, chutando a bola com uma velocidade de $20m/s$. A massa da bola é de $450g$ e a duração do chute da ordem de $0,01s$. (c) Uma pessoa de $80kg$ pula do alto de um muro de $2,5m$ de altura, caindo em pé (sem dobrar os joelhos). A duração do impacto é de $0,01s$. É melhor dobrar os joelhos! (d) Um carro de $1,5toneladas$, a $60km/h$, bate num muro. A duração do choque é de $0,1s$. 

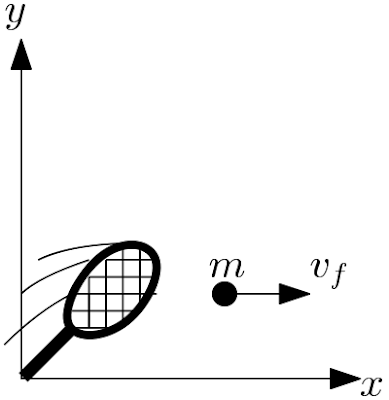
 a) Em um saque de tênis o competidor joga a bola verticalmente para cima e a acerta quanto ela chega ao seu máximo com velocidade $v_i=0$, supondo que a bola seja acetada nesse momento o momento inicial é dado por $P_i=mv_i$, após o decorrer de um tempo $\Delta t$ a bola viaja com velocidade $v_f$ para a direita a situação inicial esta ilustrada abaixo,

Dessa forma a variação de momento será dado por, $$\Delta P = mv_f-mv_i$$ Como a variação do momento é igual ao impulso $I=F\Delta t=\Delta P$ teremos que, $$F\Delta t=mv_f-mv_i\Rightarrow$$ $$F=\frac{mv_f-mv_i}{\Delta t}$$ Ou em $kgf$, $$F=\frac{mv_f-mv_i}{g\Delta t}$$ Substituindo os valores, obtemos $$F=\frac{(0,06kg)(40m/s)}{(9,8m/s^2)(0,005kg)}$$ $$F=48,9kgf$$ b) Supondo que a bola inicialmente estava em repouso, isto é, $v_i=0$, no segundo momento a bola é lançada para a direita com velocidade $v_f$,

Dessa forma a variação de momento será dado por, $$\Delta P = mv_f-mv_i$$ Como a variação do momento é igual ao impulso $I=F\Delta t=\Delta P$ teremos que, $$F\Delta t=mv_f-mv_i\Rightarrow$$ $$F=\frac{mv_f-mv_i}{\Delta t}$$ Ou em $kgf$, $$F=\frac{mv_f-mv_i}{g\Delta t}$$ Substituindo os valores, obtemos $$F=\frac{(0,45kg)(20m/s)}{(9,8m/s^2)(0,01s)}\Rightarrow$$ $$F=91,8kgf$$ c) Supondo que a pessoa pele de uma altura $h$ por conservação de energia toda sua energia potencial será transformada em cinética logo, $$mgh=\frac{1}{2}mv_i^2\Rightarrow$$ $$v_i=-\sqrt{2gh}$$ Logo existe uma força a força de impacto com o solo desacelera a pessoa ate o repouso em um tempo $\Delta t$,

Dessa forma a variação de momento será dado por, $$\Delta P = mv_f-mv_i$$ Como a variação do momento é igual ao impulso $I=F\Delta t=\Delta P$ teremos que, $$F\Delta t=mv_f-mv_i\Rightarrow$$ $$F=\frac{m\sqrt{2gh}}{\Delta t}$$ Ou em $kgf$, $$F=\frac{m\sqrt{2gh}}{g\Delta t}$$ Substituindo os valores, obtemos $$F=\frac{(80kg)\sqrt{2(9,8m/s^2)(2,5m)}}{(9,8m/s^2)(0,01s)}\Rightarrow$$ $$F=5714,3kgf$$ d) Inicialmente o carro viaja a uma velocidade $v_i$ em direção ao murro, apos colidir com o murro, o carro é desacelerado para o repouso em um tempo $\Delta t$,

Dessa forma a variação de momento será dado por, $$\Delta P = mv_f-mv_i$$ Como a variação do momento é igual ao impulso $I=F\Delta t=\Delta P$ teremos que, $$F\Delta t=mv_f-mv_i\Rightarrow$$ $$F=\frac{mv_f-mv_i}{\Delta t}$$ Ou em $kgf$, $$F=\frac{mv_f-mv_i}{g\Delta t}$$ Substituindo os valores, obtemos, $$F=\frac{(1,5\times10^3kg)(16,6m/s)}{(9,8m/s^2)(0,1s)}\Rightarrow$$ $$F=25,4\times10^3kgf$$