Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 9.2

9.2) Na teoria corpuscular da luz, no século 17, imaginava-se um feixe de luz como constituído de corpúsculos muito pequenos, movendo-se com velocidade muito elevada. A reflexão da luz num espelho seria produzida pela colisão dos corpúsculos luminosos com o mesmo, de forma análoga a uma colisão elástica com uma parede impenetrável. Ao atravessar a superfície de separação entre dois meios transparentes distintos (ar e água, por exemplo). um corpúsculo luminoso teria sua velocidade alterada pelo efeito de uma força impulsiva normal à superfície de separação, prosseguindo depois em seu movimento, livre da ação de forças. Sejam $\theta_1$ , $\theta_1'$ e $\theta_2$ os ângulos de incidência, reflexão, e refração respectivamente. Mostre que este modelo explicaria as leis da reflexão e da refração: raios refletido e refratado no plano de incidência, com $\theta_1'=\theta_1$ , $\frac{\sin\theta_1}{\sin\theta_2} =n_{12}$ , e calcule o índice de refração relativo $n_{12}$ do segundo meio em relação ao primeiro em função das velocidades $v_1$ e $v_2$ dos corpúsculos nos meios 1 e 2. A velocidade dos corpúsculos seria maior no ar ou na água? 

 Quanto a questão de provar a propriedade de reflexão, podemos tocar a aproximação descrita no problema e considerar que a luz é feita de pequenos corpúsculos que colidem de forma elástica com o solo,

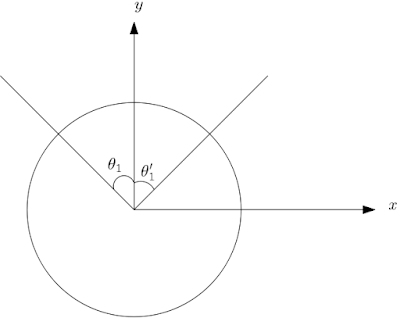
O momento inicial de um corpúsculo que se aproxima com velocidade $v_1$ do solo com ângulo de incidência $\theta_1$ é dado por, $$\vec{P}_i=mv_1\left( \sin\theta_1\hat{i} +\cos\theta_1\hat{j}\right)$$ Por outro lado após a colisão ele terá um momento dado por, $$\vec{P}_f=mv_2\left( \sin\theta_1'\hat{i} +\cos\theta_1'\hat{j}\right)$$ Supondo que o momento foi conservado teremos que, $$mv_1\left( \sin\theta_1\hat{i} +\cos\theta_1\hat{j}\right)=mv_2\left( \sin\theta_1'\hat{i} +\cos\theta_1'\hat{j}\right)$$ Dessa equação vetorial encontramos as seguintes equações, $$\left\lbrace \begin{array}{ll} v_1\cos\theta_1=v_2\cos\theta_1'\\ v_1\sin\theta_1=v_2\sin\theta_1'\\ \end{array}\right.$$ isto é, $$\left\lbrace \begin{array}{ll} \frac{v_1}{v_2}=\frac{\cos\theta_1'}{\cos\theta_1}\\ \frac{v_1}{v_2}=\frac{\sin\theta_1'}{\sin\theta_1}\\ \end{array}\right.$$ Porém como a massa é constante, e por hipótese trata-se de uma colisão elástica, para que o momento seja conservado temos que considerar que $v_1=v_2$, logo, $$\left\lbrace \begin{array}{ll} \frac{\cos\theta_1'}{\cos\theta_1}=1\\ \frac{\sin\theta_1'}{\sin\theta_1}=1\\ \end{array}\right.$$ Essas relações valem para todo $\theta_1$ e $\theta_1'$ logo, $$\theta_1=\theta_1'$$

Considerando agora que o corpúsculo incide com uma velocidade $v_1$ e ângulo $\theta_1$ e devido a um Impulso $\frac{I}=I\hat{j}$ o corpúsculo desvia sua trajetória para um ângulo $\theta_2$ provocando uma variação de momento $\Delta \vec{P}$ dessa forma teremos que, $$I\hat{j}=\Delta \vec{P}$$ A variação de momento linear é dada por, $$I\hat{j}=mv_2\left(\sin\theta_1\hat{i}+\cos\theta_1\hat{j}\right) -mv_1 \left(\sin\theta_2\hat{i}+\cos\theta_2\hat{j}\right)$$ Dessa equação vetorial obtemos, $$\left\lbrace \begin{array}{ll} I=mv_2\cos\theta_1-mv_1\cos\theta_2\\ 0=mv_2\sin\theta_1-mv_1\sin\theta_2\\ \end{array}\right.$$ A da segunda equação obtemos, $$0=mv_2\sin\theta_1-mv_1\sin\theta_2\Rightarrow$$ $$v_2\sin\theta_1=v_1\sin\theta_2\Rightarrow$$ $$\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2}$$ Note que $\theta_2>\theta_1$, logo, $\sin\theta_2<\sin\theta_1$ isso significa que $v_1>v_2$.