Moyses - Curso de Física Básica, Electromagnetismo , Problema Resolvido 6.1
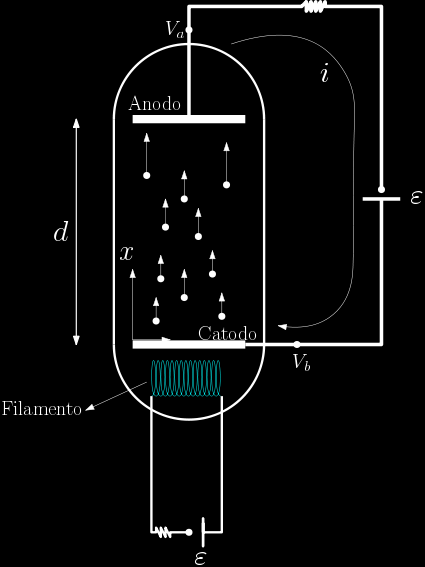
6.1) Uma válvula dioso da era pré-transistor contém um par e placas paralelas de espaçamento $d$, no vácuo. Estabelece-se entre elas uma diferença de potencial $V$. Um feixe de elétrons com área de secção transversal $A$ e de velocidade inicial $v_0$ é emitido a partir de uma das placas (cátodo) e acelerado até a outra (anodo), produzindo uma corrente estacionaria de intensidade $i$. (a) Calcule a velocidade $v(x)$ de um elétron à distância $x$ do cátodo. (b) Calcule a densidade $n(x)$ de elétrons no feixe como função de x. Suponha que $i$ é suficientemente fraco para que o campo gerado pelos elétrons seja desprezível em confronto com o campo acelerador.
(a) Primeiramente devemos notar que o campo elétrico gerado pelas placas gera uma força elétrica $F_e$ que acelera os elétrons de carga $e$ e pela segunda lei de Newton $$F_e=m_ea\Rightarrow$$ $$eE=m_ea\Rightarrow$$ $$a=\frac{eE}{m_e}$$ O potencial $V$ entre às duas placas é dado por $V=Ed$, ou seja, $E=\frac{V}{d}$, dessa forma a aceleração será $$a=\frac{eV}{m_ed}\ \ \ \ (1)$$ Adotando o referencial sobre a placa inferior e com eixo $ox$ na direção vertical podemos relacionar a velocidade $v(x)$ ao longo da distância $d$ usando a equação de Torricelli $v_f^2=v_0^2+2a\Delta x$, supondo que a velocidade com que o elétron é emitido da placa inferior é $v_0$ teremos $$v(x)^2=v_0^2+2\frac{eV}{m_ed}x\Rightarrow$$ $$v(x)=v_0\left( 1+\frac{2eVx}{m_edv_0^2}\right)^{\frac{1}{2}}\ \ \ \ (2)$$ (b) Para calcular o número $n$ de elétrons a uma distância $x$ usaremos a equação da densidade de corrente $J=nqv_d$, nesse caso a velocidade de deriva $v_d$ é dada pela equação (2) e $q=e$, logo $$J=nqv_0\left( 1+\frac{2eVx}{m_edv_0^2}\right)^{\frac{1}{2}}\Rightarrow$$ $$n(x)=\frac{J}{ev_0}\left( 1+\frac{2eVx}{m_edv_0^2}\right)^{-\frac{1}{2}}\ \ \ \ (3)$$ sendo a corrente proporcional a densidade de corrente e a área do feixe $AJ=i\Rightarrow$ $J=\frac{i}{A}$ assim a equação (3) se torna $$n(x)=\frac{i}{eAv_0}\left( 1+\frac{2eVx}{m_edv_0^2}\right)^{-\frac{1}{2}}\ \ \ \ (3)$$


Comentários