7.2) A agulha imantada do problema 1 também produz um campo magnético, que, conforme será visto no capítulo 8, só difere do campo de um dipolo elétrico $\vec{p}$ pelas substituições $\vec{p}\longrightarrow \vec{m}$, $\varepsilon_0\longrightarrow 1/\mu_0$, onde $\mu_0$ é uma constante (permeabilidade magnética do vácuo). (a) usando esse resultado, determine o campo magnético $\vec{B}$ (em módulo, direção e sentido) produzido pela agulha um ponto $P$ situado em seu prolongamento, a uma distância $d$ da agulha. (b) Suponha que, com a agulha imobilizada numa direção horizontal, perpendicular ao campo magnético $\vec{B}_0$ da terra, outra agulha imantada é trazida para o ponto $\vec{P}$ definido na parte (a), ficando sujeita aos campos $\vec{B}$ e $\vec{B}_0$. Determine o ângulo $\alpha$ entre a orientação de equilíbrio da segunda angulação e $\vec{B}_0$. Mostre que, medindo-o, pode-se determinar a razão $m/B_0$. Combinando esses resultados com o do problema 1, obtêm-se os valores de $\vec{m}$ e de $\vec{B}_0$. Esse método é devido a Gauss
a) O potencial elétrico de um dipolo em um ponto sobre o eixo $z$, como na figura, é
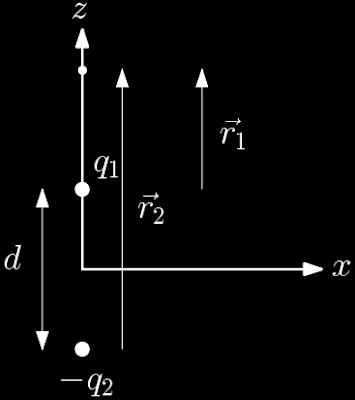
$$V=\frac{q_1}{4\pi\varepsilon_0 r_1}-\frac{q_2}{4\pi\varepsilon_0 r_2},$$ note que as cargas são iguais, isto é, $|q_1|=|q_2|$, reescrevemos $r_2$ em termos de $r_1$ com a relação $r_2=r_1+d$, dessa forma obtemos a expressão $$V=-\frac{q}{4\pi\varepsilon_0}\left[\frac{1}{(r_1+d)}-\frac{1}{r_1}\right], $$ podemos agora escrever $r_1$ para deixar tudo em função de $z$ usando a seguinte relação $r_1=z-\frac{1}{2}d$, logo $$V=-\frac{q}{4\pi\varepsilon_0}\left[\frac{1}{(z+\frac{1}{2}d)}-\frac{1}{z-\frac{1}{2}d~}\right]. $$ O campo elétrico na direção $z$ é dado por
$$E_z=-\frac{dV}{dz},$$
logo
$$E_z=\frac{q}{4\pi\varepsilon_0}\frac{d}{dz}\left[\frac{1}{(z+\frac{1}{2}d)}-\frac{1}{z-\frac{1}{2}d}\right] \Rightarrow$$
$$E_z=\frac{q}{4\pi\varepsilon_0}\left[-\frac{1}{(z+\frac{1}{2}d)^2}+\frac{1}{(z-\frac{1}{2}d)^2}\right] \Rightarrow$$
$$E_z=\frac{q}{4\pi\varepsilon_0}\left[\frac{z^2+zd+\frac{1}{4}d^2-z^2+zd-\frac{1}{4}d^2}{(z+\frac{1}{2}d)^2(z-\frac{1}{2}d)^2}\right] \Rightarrow$$
$$E_z=\frac{q}{4\pi\varepsilon_0}\left[\frac{2zd}{(z+\frac{1}{2}d)^2(z-\frac{1}{2}d)^2}\right] $$
supondo que $z>>d$ teremos
$$E_z=\frac{q}{4\pi\varepsilon_0}\left[\frac{2zd}{(z)^2(z)^2}\right] \Rightarrow$$
$$E_z=\frac{qd}{2\pi\varepsilon_0z^3} \Rightarrow$$
$$E_z=\frac{p}{2\pi\varepsilon_0z^3} $$
realizando as substituições $p=m$ e $\varepsilon_0=\frac{1}{\mu_0}$, obtemos
$$B_z=\frac{m\mu_0}{2\pi z^3} $$
b) A agulha tende a se alinhar com o campo restante $\vec{B}+\vec{B}_0=B\hat{i}+B_0\hat{j}$ dessa forma o ângulo que a agulha fará com o campo magnético da terra será o ângulo entre $\vec{B}$ e $\vec{B}+\vec{B}_0$

$$\tan\alpha=\frac{B}{B_0}=\frac{B_z}{B_0}=\frac{m\mu_0}{2\pi z^3B_0}$$




Comentários