7.1) Uma bússola tende a oscilar antes de alinhar-se com o campo magnético da terra. Considere uma agulha imantada de momento de dipolo magnético $\vec{m}$ e momento de inércia $I$, suspensa de forma a poder oscilar livremente em torno de um eixo vertical, situado em um campo magnético uniforme $\vec{B}_0$. As direções de $vec{m}$ e $\vec{B}_0$ formam inicialmente um pequeno ângulo $\theta_0$. Calcule a frequência angular de oscilação (desprezando o amortecimento) e mostre que sua determinação permite medir $|\vec{m}||\vec{B}_0|$
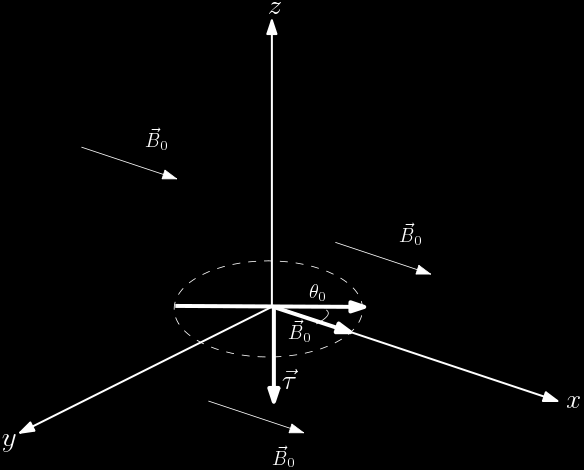
Note que o torque é dado pelo produto vetorial entre o momento de dipolo magnético com o campo magnético
$$\vec{\tau}=\vec{m}\times\vec{B}_0$$
ou de forma escalar
$$-\tau=mB_0\sin\theta$$
temos que $\tau=I\alpha$ logo
$$I\alpha=-mB_0\sin\theta\Rightarrow$$
$$\alpha=-\frac{mB_0}{I}\sin\theta$$
para um ângulo $\theta$ muito pequeno teremos
$$\alpha=-\frac{mB_0}{I}\theta\Rightarrow$$
$$\frac{d^2\theta}{dt}+\frac{mB_0}{I}\theta=0$$
podemos supor que a solução dessa equação é da forma $\theta=\sin\omega t$, logo
$$\frac{d^2}{dt^2}\left[\sin\omega t\right] +\frac{mB_0}{I}\sin\omega t=0\Rightarrow$$
$$\frac{d}{dt}\left[\omega\cos\omega t\right] +\frac{mB_0}{I}\sin\omega t=0\Rightarrow$$
$$-\omega^2\sin\omega t +\frac{mB_0}{I}\sin\omega t=0\Rightarrow$$
$$-\omega^2 +\frac{mB_0}{I}=0\Rightarrow$$
$$\omega^2 =\frac{mB_0}{I}\Rightarrow$$
$$\omega=\sqrt{\frac{mB_0}{I}}$$
sendo a frequência dada por $f=\frac{1}{2\pi}\omega$
$$f=\frac{1}{2\pi}\sqrt{\frac{mB_0}{I}}$$



Comentários