6.8) Quando uma bateria de fem igual a $1,5V$ fornece uma corrente de $1A$ a uma resistência $R$, a tenção medida entre seus terminais caem para $1,4V$. (a) Qual é o valor de $R$? (b) qual é a resistência interna da bateria? (c) qual é a taxa de conversão de energia química em energia elétrica da bateria, por unidade de tempo, nessas condições? (d) qual é a potência convertida em calor na resistência? (e) qual é a perda de potência na bateria?
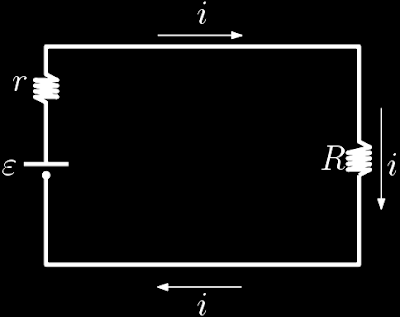
(a) temos que $V_{ab}=Ri$ logo
$$R=\frac{V_{ab}}{i}\ \ \ \ (1)$$
(b) A integral do potencial ao longo do circuito fechado é nula e dada por
$$\varepsilon-ri-Ri=0$$
explicitando $r$ obtemos
$$r=\frac{\varepsilon}{i}-R$$
substituindo (1) na equação obtemos
$$r=\frac{\varepsilon}{i}-\frac{V_{ab}}{i}.\ \ \ \ (2)$$
(c) A potência P_b da bateria é dada por $P_b=Vi$ logo
$$P_b=\varepsilon i\ \ \ \ (3)$$
(d) A potência $P_R$ dissipada pelo resistor $R$ é dada por $P_R=Vi$ sendo $V=Ri$ obtemos
$$P_R=Ri^2.$$
Substituindo (1) obtemos
$$P_R=V_{ab}i\ \ \ \ (4)$$
(e) A perda de potência na bateria é dada pela energia dissipada pela resistência interna $r$, ou seja, $P_r=Vi$ sendo o potencial $V=ri$
$$P_r=ri^2.$$
Substituindo (2) obtemos
$$P_r=\varepsilon i-V_{ab}i.\ \ \ \ \ (5)$$
As equações (1), (2), (3), (4) e (5) nos dão as respostas do problema
$$\begin{array}{lllll}
(a)&R=\frac{V_{ab}}{i}\\
(b)&r=\frac{\varepsilon}{i}-\frac{V_{ab}}{i}\\
(c)&P_b=\varepsilon i\\
(d)&P_R=V_{ab}i\\
(e)&P_r=\varepsilon i-V_{ab}i\\
\end{array}$$
Substituindo os valores do problema obtemos
$$\begin{array}{lllll}
(a)&R=1,4\Omega \\
(b)&r=0,1\Omega \\
(c)&P_b=1,5W\\
(d)&P_R=1,4W\\
(e)&P_r=0,1W\\
\end{array}$$



Comentários