Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 5.18

5.18) Um trem atravessa uma curva de raio de curvatura igual a 100 m a 30 km/h. A distância entre os trilhos é de 1 m. De que altura é preciso levantar o trilho externo para minimizar a pressão que o trem exerce sobre ele ao passar pela curva?

 Para descobrir a altura máxima que minimiza a pressão sobre o trilho, isto é, altura que minimiza a força normal preservando o caráter estático do sistema. Adotando o sistema de referencial sobre o trilho teremos,

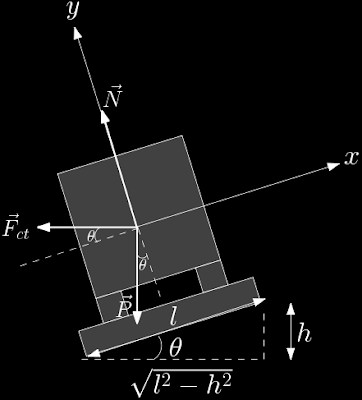
A força centrípeta $\vec{F}_{ct}$ mantém o trem na curva, enquanto a força normal que o solo faz sobre o trem evita que o veículo afunde na rampa devido a sua força peso, $$\left\lbrace \begin{array}{ll} N-P_y+F_{cty}=0\\ -F_{ctx}-P_x=0\\ \end{array}\right.$$ Decompondo os vetores obtemos, $$\left\lbrace \begin{array}{ll} N-P\cos\theta+F_{ct}\sin\theta=0\ \ \ \ (1)\\ -F_{ct}\cos\theta -P\sin\theta=0\ \ \ \ (2)\\ \end{array}\right.$$ Usando a segunda equação obtemos que, $$-F_{ct}\cos\theta=P\sin\theta\Rightarrow$$ $$-m\frac{v^2}{R}\cos\theta=mg\sin\theta\Rightarrow$$ $$-m\frac{v^2}{R}=mg\tan\theta\Rightarrow$$ $$v^2=-gR\tan\theta\ \ \ \ (3)$$ Olhando para o triângulo retângulo formado pela abertura da inclinação dos trilhos obtemos que $\tan\theta=\frac{h}{\sqrt{l^2-h^2}}$, aplicando o resultado na equação (3), $$v^2=-gR\frac{h}{\sqrt{l^2-h^2}}\Rightarrow$$ $$v^2\sqrt{l^2-h^2}=-gRh\Rightarrow$$ $$v^4(l^2-h^2)=g^2R^2h^2\Rightarrow$$ $$v^4l^2-v^4h^2=g^2R^2h^2\Rightarrow$$ $$v^4l^2=(g^2R^2+v^4)h^2\Rightarrow$$ $$\frac{v^4l^2}{(g^2R^2+v^4)}=h^2\Rightarrow$$ $$h=\frac{v^2l}{\sqrt{g^2R^2+v^4}}$$ Substituindo os valores adequadamente obtemos, $$h=\frac{(8,3m,s)^2(1m)}{\sqrt{(9,8m/s^2)^2(100m)^2+(8,3m,s)^4}}=0,071 m$$ $$h=7,1cm$$