Problema de cinemática de rotação

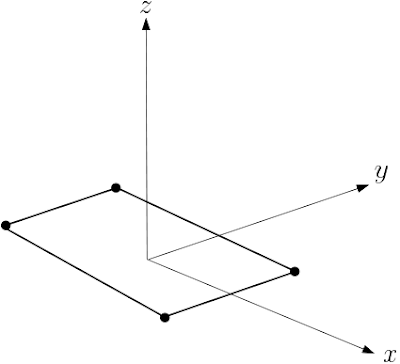
Na figura ao lado todas as massas são iguais e as hastes entre as partículas tem massas desprezíveis a) Encontre o centro de massa do sistema. b) Achar o momento de inercia em relação ao eixo z. c) Se o sistema inicia um movimento de rotação em torno da origem com velocidade angular de 0.5s, qual eh a energia cinética do sistema?

Escolheremos o sistema de referencial sobre a esfera a esquerda da base como na figura,

a) Sabemos que que o centro de massa de um conjunto de massas é dado por, $$\vec{P}_{cm}=\frac{1}{\sum_{i=1}^{n}m_i}\sum_{i=1}^{n}m_i\vec{r}_i$$ Como todas as massa são iguais temos que, $$\vec{P}_{cm}=\frac{m}{4m}\sum_{i=1}^{n}\vec{r}_i$$ ou seja, $$\vec{P}_{cm}=\frac{1}{4}\sum_{i=1}^{n}\vec{r}_i$$ Dessa forma o centro de massa $\vec{P}_{cm}$ fica totalmente definido pela soma dos vetores posição de cada massa, em relação ao sistema de referencial escolhido, logo, $$\vec{P}_{cm}=\frac{1}{4}\left[ (0\hat{i}+0\hat{j})+(0\hat{i}+\frac{l}{2}\hat{j})+(l\hat{i}+0\hat{j})+(l\hat{i}+\frac{l}{2}\hat{j})\right]$$ Somando os vetores obtemos, $$\vec{P}_{cm}=\frac{1}{4}\left[2l\hat{i}+l\hat{j}\right]$$ Ou seja o centro de massa está no plano $xy$ em um ponto que dista igualmente de cada esfera,  $$\left\lbrace \begin{array}{ll} x=\frac{l}{2}\\ y=\frac{l}{4}\\ \end{array}\right.$$   b) Adotando o eixo de rotação $z$ passando pelo centro de massa $\vec{P}_{cm}$

podemos calcular o momento de inercia que é dado por, $$I=\sum_{i=1}^{n}m_ir^2_i$$ Como as massa são iguais o somatório se resume a, $$I=m\sum_{i=1}^{n}r^2_i$$ Como o eixo de rotação está sobre o centro de massa que dista igualmente das esferas, basta calcular a metade da diagonal $\frac{r}{2}$ do retângulo que é dado pelo teorema de Pitagoras, $\frac{r^2}{4}=\frac{l^2}{4}+\frac{l^2}{16}=\frac{5l^2}{16}\Rightarrow r=\frac{\sqrt{5}l}{2}$ aplicando na equação obtemos, $$I=m(\frac{5l^2}{4}+\frac{5l^2}{4}+\frac{5l^2}{4}+\frac{5l^2}{4})=m5l^2$$ Logo, $$I=m5l^2\ \ \ (1)$$ c) A energia cinética na rotação é dada por, $E_c=\frac{I\omega^2}{2}$, aplicando a equação (1) obtemos, $$E_c=\frac{m5l^2\omega^2}{2}\Rightarrow$$ Aplicando o valor de $\omega$ $$E_c=\frac{5ml^2}{8}$$