5.19) No sistema da figura 1, a bolinha de massa $m$ está amarrada por fios de massa desprezível ao eixo vertical $AB$ e gira com velocidade angular $\omega$ em torno desse eixo. A distância $AB$ vale $l$. Calcule as tensões nos fios superior e inferior. Para que valor de $\omega$ o fio inferior ficaria frouxo?
A força centrifuga empurra a bola para longe do bastão enquanto o peso pucha a bolinha para a base, em contrapartida, as tensões $T_1$ e $T_2$ equilibram as demais forças deixando a bola em equilíbrio,
Adotando o referencial paralelo ao eixo $AB$ obtemos o seguinte diagrama,
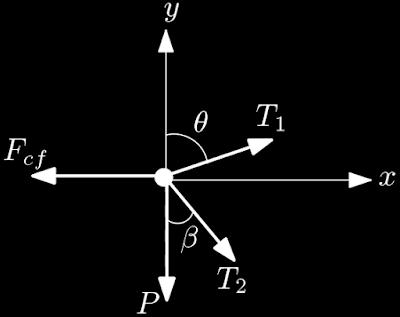
O diagrama de força será dado por,
$$\left\lbrace \begin{array}{ll}
T_{1y}-T_{2y}-P=0\\
T_{1x}+T_{2x}-F_{cf}=0\\
\end{array}\right. $$
Decompondo os vetores obtemos $$\left\lbrace \begin{array}{ll}
T_{1}\cos\theta-T_{2}\cos\beta-P=0\\
T_{1}\sin\theta+T_{2}\sin\beta-F_{cf}=0\\
\end{array}\right. $$
Reescrevendo as equações obtemos,
$$\left\lbrace \begin{array}{ll}
T_{1}-T_{2}\frac{\cos\beta}{\cos\theta}-\frac{P}{\cos\theta}=0\ \ \ (1)\\
-T_{1}-T_{2}\frac{\sin\beta}{\sin\theta}+\frac{F_{cf}}{\sin\theta}=0\ \ \ (2)\\
\end{array}\right. $$
Somando as equações obtemos,
$$-T_{2}\frac{\cos\beta}{\cos\theta}-T_{2}\frac{\sin\beta}{\sin\theta}+\frac{F_{cf}}{\sin\theta}-\frac{P}{\cos\theta}=0\Rightarrow$$
$$T_{2}\left( \frac{\cos\beta}{\cos\theta}+\frac{\sin\beta}{\sin\theta}\right) =\frac{F_{cf}\cos\theta-P\sin\theta}{\sin\theta\cos\theta}\Rightarrow$$
$$T_{2}=\frac{F_{cf}\cos\theta-P\sin\theta}{\sin\theta\cos\beta+\sin\beta\cos\theta}\ \ \ \ (3)$$
Substituindo (3) em (1) obtemos, $T_1$
$$T_{1}= \frac{F_{cf}\cos\beta+P\sin\beta}{\sin\theta\cos\beta+\sin\beta\cos\theta}\ \ \ \ (4)$$
Sendo assim resta o seguinte sistema,
$$\left\lbrace \begin{array}{ll}
T_{1}= \frac{F_{cf}\cos\beta+P\sin\beta}{\sin\theta\cos\beta+\sin\beta\cos\theta}\\
T_{2}=\frac{F_{cf}\cos\theta-P\sin\theta}{\sin\theta\cos\beta+\sin\beta\cos\theta}\\
\end{array}\right. $$
Desenvolvendo as equações do sistema obtemos,
$$\left\lbrace \begin{array}{ll}
T_{1}=m\frac{\omega^2R\cos\beta+g\sin\beta}{\sin\theta\cos\beta+\sin\beta\cos\theta}\ \ \ \ (5)\\
T_{2}=m\frac{\omega^2R\cos\theta-g\sin\theta}{\sin\theta\cos\beta+\sin\beta\cos\theta}\ \ \ \ (6)\\
\end{array}\right. $$
Devemos agora encontrar o valor de $R$ em função de $\beta$, $\theta$ e $l$, sabemos que $$\left\lbrace \begin{array}{ll}
\overline{AO}=\frac{R}{\tan\theta}\\
\overline{OB}=\frac{R}{\tan\beta}
\end{array}\right. $$
Como $l=\overline{OB}+\overline{AO}$ teremos que,
$$l=\frac{R}{\tan\beta}+\frac{R}{\tan\theta}\Rightarrow$$
$$R=\left(\frac{\sin\beta\sin\theta}{\cos\beta\sin\theta+\sin\beta\cos\theta}\right)l\ \ \ \ (7)$$
Substituindo (7) em (5) e (6) obtemos,
$$\left\lbrace \begin{array}{ll}
T_{1}=m\sin\beta\left( \frac
{\omega^2l\sin\theta\cos\beta+(\cos\beta\sin\theta+\sin\beta\cos\theta)g}
{(\sin\theta\cos\beta+\sin\beta\cos\theta)^2}\right)\\
T_{2}=m\sin\theta\left( \frac
{\omega^2l\sin\beta\cos\theta-(\sin\theta\cos\beta+\sin\beta\cos\theta)g}
{(\sin\theta\cos\beta+\sin\beta\cos\theta)^2}\right)\\
\end{array}\right. $$
Queremos agora descobrir qual é a velocidade angula $\omega_0$ para a qual o fio inferior fica frouxo, em outras palavras, a velocidade angular para a qual $T_2=0$,
$$T_{2}=m\sin\theta\left( \frac
{\omega_0^2l\sin\beta\cos\theta-(\sin\theta\cos\beta+\sin\beta\cos\theta)g}
{(\sin\theta\cos\beta+\sin\beta\cos\theta)^2}\right)=0\Rightarrow$$
$$\omega_0^2l\sin\beta\cos\theta-(\sin\theta\cos\beta+\sin\beta\cos\theta)g=0\Rightarrow$$
$$\omega_0^2=\frac{(\sin\theta\cos\beta+\sin\beta\cos\theta)g}{l\sin\beta\cos\theta}\Rightarrow$$
$$\omega_0=\sqrt{\frac{(\sin\theta\cos\beta+\sin\beta\cos\theta)g}{l\sin\beta\cos\theta}}$$
Logo, as tensões e a velocidade angular crítica é,
$$\left\lbrace \begin{array}{lll}
T_{1}=m\sin\beta\left( \frac
{\omega^2l\sin\theta\cos\beta+(\cos\beta\sin\theta+\sin\beta\cos\theta)g}
{(\sin\theta\cos\beta+\sin\beta\cos\theta)^2}\right)\\
T_{2}=m\sin\theta\left( \frac
{\omega^2l\sin\beta\cos\theta-(\sin\theta\cos\beta+\sin\beta\cos\theta)g}
{(\sin\theta\cos\beta+\sin\beta\cos\theta)^2}\right)\\
\omega_0=\sqrt{\frac{(\sin\theta\cos\beta+\sin\beta\cos\theta)g}{l\sin\beta\cos\theta}}\\
\end{array}\right. $$
Substituindo os valores do problema obtemos,
$$\left\lbrace \begin{array}{lll}
T_{1}=\frac{m}{2}\left(\frac{3}{4}\omega^2l+g\right)\\
T_{2}=\frac{m}{2}\sqrt{3}\left( \frac{1}{4}\omega^2l-g\right)\\
\omega_0=2\sqrt{\frac{g}{l}}\\
\end{array}\right. $$
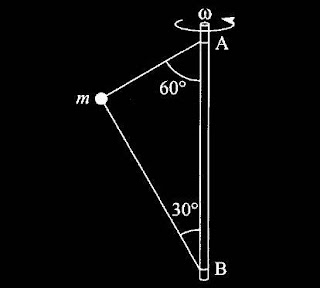




Comentários