Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 5.20

5.20) Um feixe de elétrons de velocidade $3\cdot10^{6}m/s$ penetra horizontalmente na região entre um par de placas defletoras de $2cm$ de extensão, onde existe um campo elétrico vertical de $1kV/m$. Calcule o ângulo de deflexão e a magnitude da velocidade do feixe ao emergir da região entre as placas.

 Vamos supor que a placa superior é negativa enquanto a placa inferior é positiva, como o elétron tem carga negativa $-q$ veremos uma trajetória parabólica decrescente que desvia o caminho original por uma distância $y_l$, o elétron sairá com um ângulo $\theta$ em relação à horizontal, com uma velocidade $\vec{v}$, maior da velocidade inicial $v_0\hat{k}$, pois, agora a velocidade terá uma velocidade com uma componente em $y$ causada pelo campo elétrico $-E\hat{j}$, desconsideraremos fatores como o campo gravitacional e o efeito de distorção do campo elétrico na borda das placas,

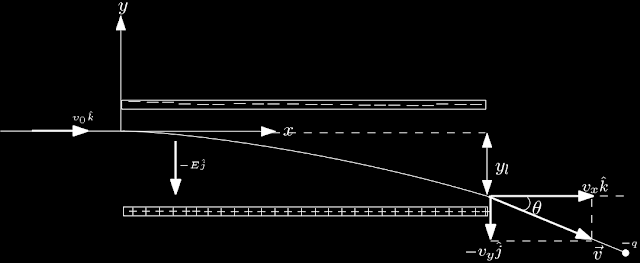
Como podemos ver na figura 1 adotamos o referencial na entrada da placa na direção do movimento inicial, dessa forma as equações do movimento do elétron é da forma, $$\left\lbrace \begin{array}{ll} x=v_0t\\ y=-\frac{1}{2}at^2\\ \end{array}\right.$$ A aceleração pode ser escrita em termos de força usando a segunda lei de Newton, $a=\frac{F}{m}$, porém, a força em questão é a força elétrica dada em modulo por, $F=(-q)(-E)=qE$, ou seja, $a=\frac{qE}{m}$, sendo assim as equações do movimento são dadas por, $$\left\lbrace \begin{array}{ll} x=v_0t\ \ \ \ (1)\\ y=-\frac{1}{2}\frac{qE}{m}t^2\ \ \ \ (2)\\ \end{array}\right.$$ Podemos ver na figura 1 que o ângulo $\theta$ é dado por, $$\tan\theta=\frac{-v_y}{v_x}\ \ \ (3)$$ A velocidade é encontrada derivando as equações (1) e (2) em relação ao tempo, $$\left\lbrace \begin{array}{ll} v_x=v_0\\ v_y=-\frac{qE}{m}t\\ \end{array}\right.$$ Substituindo as equações de $v_x$ e $v_y$ em (3) obtemos, $$\tan\theta=\frac{qE}{mv_0}t\ \ \ (4)$$ A equação (4) nos da o ângulo em relação à horizontal que é diretamente proporcional ao tempo, como a extensão da placa é $l$ o elétron percorrerá a placa em um intervalo de tempo dado por (1) $t=\frac{l}{v_0}$, aplicando o tempo na equação 4 obtemos $\theta$, $$\tan\theta=\frac{qEl}{mv_0^2}\Rightarrow$$ $$\theta=\arctan\left( \frac{qEl}{mv_0^2}\right)\ \ \ (5)$$ Já a velocidade de saída é dado por $$|\vec{v}|=\sqrt{v_x^2+v_y^2}\Rightarrow$$ $$|\vec{v}|=\sqrt{v_0^2+\left( -\frac{qE}{m}t\right) ^2}$$ Onde $t=\frac{l}{v_0}$, logo o ângulo e a velocidade de saída serão, $$\left\lbrace \begin{array}{ll} \theta=\arctan\left( \frac{qEl}{mv_0^2}\right)\\ |\vec{v}|=\sqrt{v_0^2+\left( \frac{qEl}{mv_0}\right) ^2}\\ \end{array}\right.$$