Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 6.3
6.3) Uma partícula de massa $m=1kgo$, lançado sobre um trilho retilíneo com velocidade de $3m/s$, está sujeita a uma força $F(x)=-a-bx$, onde $a=4N$, $b=1N/m$ e x é o deslocamento, em m, a partir da posição inicial. (a) Em que pontos do trilho a velocidade da partícula se anula? (b) Faça o gráfico da velocidade da partícula entre esses pontos. (C) A que tipo de lei de forças corresponde $F(x)$?
Como é uma força que atua em função da distância que a partícula percorre podemos calcular o trabalho $W=\sum_{i=0}^{f}F(x_i)\Delta x_i$ que nada mais é do que a soma da força multiplicada pelos deslocamentos infinitesimais da partícula de uma posição de $x_0=0$ até $x_f=x$, logo, $$W=\int_{x_0}^{x}F(u)du$$, porém, o trabalho realizado é proporcional a diferença de energia cinética dessa da partícula, logo, $$\int_{x_0}^{x}\left( -a-bu\right) du=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\Rightarrow$$ $$-ax-\frac{1}{2}bx^2+ax_0+\frac{1}{2}bx_0^2=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2$$ Explicitando $v$ encontramos a função que descreve a velocidade da partícula em função da posição $x$, $$-ax-\frac{1}{2}bx^2+ax_0+\frac{1}{2}bx_0^2=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\Rightarrow$$ $$2a(x_0-x)+b(x_0^2-x^2)=mv^2-mv_0^2\Rightarrow$$ $$\frac{2a}{m}(x_0-x)+\frac{b}{m}(x_0^2-x^2)+v_0^2=v^2\Rightarrow$$ $$v=\pm\sqrt{\frac{2a}{m}(x_0-x)+\frac{b}{m}(x_0^2-x^2)+v_0^2}\ \ \ \ (1)$$ Para descobrir os valores de $x$ para os quais a velocidade da partícula anula-se devemos resolver a equação de segundo gral de dentro da rais de $v$, $$\frac{2a}{m}(x_0-x)+\frac{b}{m}(x_0^2-x^2)+v_0^2=0\Rightarrow$$ $$x^2+\frac{2a}{b}x-(\frac{2a}{b}x_0+x_0^2+\frac{m}{b}v_0^2)=0\ \ \ (2)$$ As soluções da equação (2) são, $$\left\lbrace \begin{array}{lll} x_{max}=-\frac{a}{b}+\sqrt{\frac{a^2}{b^2}+\frac{2a}{b}x_0+x_0^2+\frac{m}{b}v_0^2}\\ x_{min}=-\frac{a}{b}-\sqrt{\frac{a^2}{b^2}+\frac{2a}{b}x_0+x_0^2+\frac{m}{b}v_0^2}\\ \end{array}\right. $$ Substituindo os valores, $$\left\lbrace \begin{array}{lll} x_{max}=1m\\ x_{min}=-9m\\ \end{array}\right. $$ Substituindo os valores em (1) encontramos a equação $$v=\pm\sqrt{9-8x-x^2}$$ Essa função é representada pelo gráfico $v\times x $ dado por,
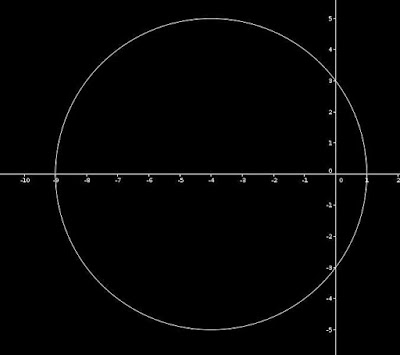


Comentários