Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 7.15

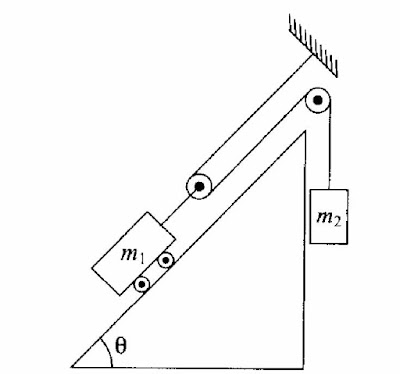
7.15) Um vagão de massa $m_1=4$toneladas está sobre um plano inclinado de inclinação $\theta=45°$, ligado a uma massa suspensa $m_2=500kg$ pelo sistema de cabo e polias ilustrado na Fig. Supõe-se que o cabo é inextensível e que a massa do cabo e das pólias é desprezível em confronto com as demais. O coeficiente de atrito cinético entre o vagão e o plano inclinado é $\mu_c=0,5$ (Na verdade $\mu_e$) e o sistema é solto do repouso. (a) Determine as relações entre os deslocamentos $s_1$ e $s_2$ e as velocidades $v_1$ e $v_2$ das massas $m_1$ e $m_2$, respectivamente. (b) Utilizando a conservação da energia, calcule de que distância o vagão se terá deslocado ao longo do plano inclinado quando sua velocidade atingir $4,5km/h$.

a) Examinando mais atentamente a corda, concluímos que, devido ao fato dela ser inextensível o comprimento $C$ da corda é constante,

Logo os comprimentos demarcados na imagem podem ser usados para descrever o comprimento da corda, $$2S_1+S_2=C$$ Como a corda é constante podemos representar uma variação da corda e obter o vínculo do sistema, $$2\Delta S_1+\Delta S_2=0$$ Dividindo a expressão pela variação do tempo e tomando as quantidades infinitesimais obtemos $$2v_1+v_2=0$$ Ou seja $$\left\lbrace \begin{array}{ll} \Delta S_2=-2\Delta S_1\ \ \ (1)\\ v_2=-2v_1\ \ \ \ \ \ \ \ \ (2)\\ \end{array}\right.$$ b) Adotaremos o referencial sobre a pólia no topo da rampa com eixo $ox$ positivo orientado sobre a rampa,

Podemos então representar as forças que atuam sobre os blocos de massa $m_1$, e obter, $$\left\lbrace \begin{array}{ll} N_1-P_1\cos\theta=0\ \ \ \ (3)\\ 2T-P_1\sin\theta-F_a=m_1a_1\ \ \ \ (4)\\ \end{array}\right.$$ Para descobrir qual sera a distância $\Delta S_1$ que o carrinho de massa $m_1$ percorre podemos usar conservação de energia, a energia inicial do sistema deve ser igual à energia final, porém, como a energia do sistema não se conserva já que parte é liberado como trabalho devido à força de atrito, a energia inicial deve ser igual à final mais o trabalho realizado pelo sistema, $$E_i=E_f+W\ \ \ (5)$$ Supondo que inicialmente o sistema esteja em repouso, $$E_i=m_1gh_1+m_2gh_2\ \ \ (6)$$ Ao final do movimento a energia final será, $$E_f=m_1gh'_1+m_2gh'_2+\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2\ \ \ (7)$$ Enquanto o trabalho é realizado pela força de atrito $-F_a$ que pode ser obtida pela equação (3), $$W=\left( -P_1\right) \mu_e\cos\theta\left( -\Delta S_1\right)$$ $$W=P_1\mu_e\cos\theta\Delta S_1 \ \ \ \ (8)$$ Substituindo (7), (6) e (8) na equação (5) obtemos, $$m_1gh_1+m_2gh_2=m_1gh'_1+m_2gh'_2+\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2-P_1\mu_e\cos\theta\Delta S_1$$ Olhando novamente para a última figura, mais especificamente para o triangulo de abertura $\theta$ formados pelos lados $S_1$ e $h_1$, encontramos a altura inicial do bloco de massa $m_1$, $h_1=-S_1\sin\theta$, enquanto a altura inicial do bloco de massa $m_2$ é $h_2=-S_2$ aplicando tais conclusões na última equação, $$-m_1gS_1\sin\theta-m_2gS_2=m_1gh'_1+m_2gh'_2+\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+P_1\mu_e\cos\theta\Delta S_1$$ Por outro lado, é natural esperar que as alturas finais $h'_1$ e $h'_2$ sejam dadas pelas variações $-\Delta S_1$ e $-\Delta S_2$ de $-S_1$ e $-S_2$, respectivamente, logo, $$-m_1gS_1\sin\theta-m_2gS_2=m_1g\left( -\Delta S_1-S_1\right)\sin\theta +m_2g\left( -\Delta S_2-S_2 \right) +\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+P_1\mu_e\cos\theta\Delta S_1$$ Reorganizando a equação obtemos, $$0=-m_1g\Delta S_1\sin\theta -m_2g\Delta S_2+\frac{1}{2}m_1v_1^2+\frac{1}{2}m_2v_2^2+m_1g\mu_e\cos\theta\Delta S_1$$ Usando as equações (1) e (2) que descreve a relação entre as posições e velocidades entre $m_1$ e $m_2$, $$0=-m_1g\Delta S_1\sin\theta +2m_2g\Delta S_1+\frac{1}{2}m_1v_1^2+2m_2v_1^2+m_1g\mu_e\cos\theta\Delta S_1$$ Explicitando $\Delta S_1$ obtemos, $$\Delta S_1=\frac{\left(m_1+4m_2\right) v_1^2}{2\left( m_1g\sin\theta-m_1g\mu_e\cos\theta-2m_2g\right) }$$ Substituindo os valores do problema obtemos, $$\Delta S_1=\frac{\left((4000kg)+4(500kg)\right) (1,25m/s)^2}{2\left( (4000kg)\sin(45°)-(4000kg)(0,5)\cos(45°)-2(500kg)\right)(9,8) }\Rightarrow$$ $$1,15m$$