Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.12

8.12) Calcule as coordenadas do $CM$ da placa homogênea indicada na figura, um círculo de $1,0m$ de raio do qual foi removido um círculo de $0,5m$ de raio, com uma separação de $0,25m$ entre os centros $O$ e $O'$ dos dois círculos.

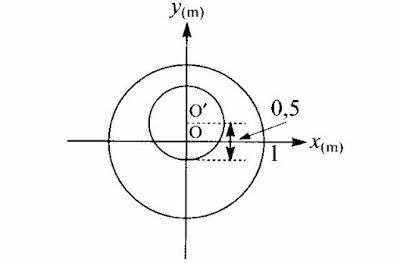
Usando o referencial que está na figura podemos representar o centro de massa da figura encontra-se no ponto $(0,0)$ enquanto o centro de massa que foi retirado da figura está na posição $(0,0.25)$, note que a área de figura maior $A_1$ é, $$A_1=\pi R^2=\pi\ \ \ (1)$$ Enquanto que ao círculo menor que foi retirado do maior tem área dada por, $$A_1=\pi R^2=\pi(0,5)^2=\frac{\pi}{4}\ \ \ (2)$$ Supondo que a massa está uniformemente distribuída sobre o círculo então a massa $m_1$ e $m_2$ do maior e do menor círculo, respectivamente, são danos por (1) e (2), $$\left\lbrace \begin{array}{ll} m_1=m\pi\\ m_2=m\frac{\pi}{4}\\ \end{array}\right.$$ Dessa forma podemos encontrar o centro de massa análogo ao que foi feito na questão (8.11), $$\vec{C}_m=\frac{1}{m\left( \pi-\frac{\pi}{4}\right) }\left[m\pi\left( 0,0\right) -m\frac{\pi}{4}\left( 0,\frac{1}{4}\right) \right]$$ Resolvendo a equação concluímos que o centro de massa está em, $$\vec{C}_m=\left(0,\frac{1}{12}\right)$$