Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.2

8.2) Um atirador, com um rifle de $2kg$ apoiado ao ombro, dispara uma bala de $15g$, cuja velocidade na boca da arma (extremidade do cano) é de $800m/s$. (a) Com que velocidade inicial a arma recua? (b) Que impulso transmite ao ombro do atirador? (c) Se o recuo é absorvido pelo ombro em $0,05s$, qual é a força média exercida sobre ele, em N e em $kgf$?


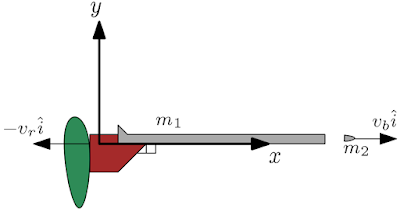
a) Adotando o referencial no cano do rifle de massa $m_r$, com eixo $ox$ sobre o cano,

Como inicialmente o o rifle está em repouso o momento no instante inicial é nulo, $\vec{P}_i=0$

No segundo momento o rifle adquire uma velocidade $-v_r\hat{i}$ enquanto a bala adquire uma velocidade $v_b\hat{i}$ logo o momento total final $\vec{P}_f$ é dado por, $$\vec{P}_f=-m_rv_r\hat{i}+m_bv_b\hat{i}$$ Como o momento total do sistema se conserva teremos que, $$0=-m_rv_r+m_bv_b$$ Explicitando $v_r$ obtemos, $$v_r=\frac{m_b}{m_r}v_b\ \ \ (1)$$ b) O impulso $\vec{I}$ é proporcional a variação do momento, como inicialmente o rifle está em repouso, a variação do momento é simplesmente o momento adquirido pelo rifle, $$\vec{I}=-m_rv_r\hat{i}\Rightarrow$$ $$\vec{I}=-m_r\frac{m_b}{m_r}v_b\hat{i}\Rightarrow$$ $$\vec{I}=-m_bv_b\hat{i}\ \ \ (2)$$ c) Sabendo que o impulso $\vec{I}$ é dado pela força $\vec{F}$ multiplicado pelo intervalo de tempo $\Delta t$ teremos que, $$\vec{F}\Delta t=-m_bv_b\hat{i}$$ Explicitando $\vec{F}$ obtemos, $$\vec{F}=-\frac{m_bv_b}{\Delta t}\hat{i}\ \ \ (3)$$ obtemos os resultados (1), (2) e (3) logo, $$\left\lbrace \begin{array}{lll} a)\ v_r=\frac{m_b}{m_r}v_b\\ b)\ \vec{I}=-m_bv_b\hat{i}\\ c)\ \vec{F}=-\frac{m_bv_b}{\Delta t}\hat{i}\\ \end{array}\right.$$ Substituindo os valores do problema obtemos, $$\left\lbrace \begin{array}{lll} a)\ v_r=6m/s\\ b)\ \vec{I}=(-12N.s)\hat{i}\\ c)\ \vec{F}=(-240N)\hat{i}\ \ ou\ \ (-24,5kgf)\hat{i}\\ \end{array}\right.$$