Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 7.17

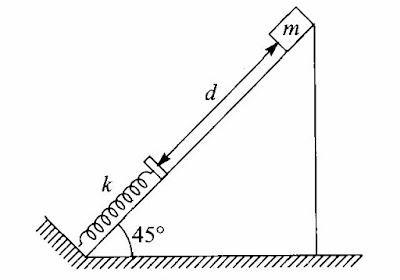
7.17) Um bloco de massa $m=10kg$ é solto em repouso do alto de um plano inclinado de $45°$ em relação ao plano horizontal, com coeficiente de atrito cinético $\mu_c=0,5$. Depois de percorrer uma distância $d=2m$ ao longo do plano, o bloco colide com uma mola de constante $k=800 N/m$, de massa desprezível, que se encontrava relaxada. (a) Qual é a compressão sofrida pela mola? (b) Qual é a energia dissipada pelo atrito durante o trajeto do bloco desde o alto do plano até a compressão máxima da mola? Que fração representa da variação total de energia potencial durante o trajeto? (c) Se o coeficiente de atrito estático com o plano é $\mu_e=0,8$, que acontece com o bloco logo após colidir com a mola?

a) Adotando o referencial no ponto de equilíbrio com eixo $ox$ na direção da inclinação da rampa,

Todas as forças que atuam sobre o bloco está representada na figura, podemos decompor o peso $\vec{P}$ do bloco na direção y e obter a normal $N$ usando a segunda lei de Newton, já que nessa direção a força resultante é nula teremos, $N-P\cos\theta=0$, como a força de atrito é dada por $F_a=N\mu_c$ então, $F_a=P\cos\theta\mu_c$, sabendo que o bloco vai percorrer uma distância $l=d+\Delta x$, podemos concluir que a energia total dissipada $E_d$ pelo sistema durante o movimento até o ponto $x=0$ do referencial adotado será o trabalho $W$ realizado pela força de atrito em foma de calor,

$$W=mg\mu_c\left( d+\Delta x\right)\cos\theta\ \ \ \ (1)$$

A energia que o bloco tem antes de descer a rampa é apenas a energia potencial do sistema em função da altura $h$, para determinar a altura devemos olhar para o triângulo retângulo de cateto $h$ e hipotenusa $d+\Delta x$, como esse triângulo é semelhante ao triângulo determinado pela rampa, o ângulo oposto a $h$ é $\theta$, logo a relação $\sin\theta$ fornece a altura, $h=(d+\Delta x)\sin\theta$, dessa forma a energia inicial $E_i$ do sistema será,

$$E_i=mg(d+\Delta x)\sin\theta\ \ \ \ (2)$$

Ao descer a rampa e percorrer a distância $d+\Delta x$ o bloco terá energia potencial elástica e nem um potencial gravitacional visto que o referencial colocado no ponto de compressão máxima da mola representa o ponto zero de energia potencial gravitacional, sendo assim a energia final $E_f$ do sistema será,

$$E_f=\frac{1}{2}k\left( \Delta x\right) ^2\ \ \ \ (3)$$

Como ja foi dito o sistema durante o movimento dissipa a energia inicial $E_i$ de forma que $E_f<E_i$, para corrigir tal diferença somamos a energia final o trabalho realizado pelo mesmo, logo,

$$E_i=E_f+W\ \ \ \ (4)$$

Substituindo as equações (1), (2) e (3) na relação (4) obtemos,

$$mg(d+\Delta x)\sin\theta=\frac{1}{2}k\left( \Delta x\right) ^2+mg\mu_c\left( d+\Delta x\right)\cos\theta$$

Reescrevendo a equação obtemos, a equação de segundo gral,

$$\frac{1}{2}\left( \Delta x\right) ^2+\frac{mg}{k}\left( \mu_c\cos\theta-\sin\theta\right)\Delta x +\frac{mg}{k}d\left( \mu_c\cos\theta-\sin\theta\right)=0$$

Resolvendo a equação obtemos as soluções,


$$\Delta x=\frac{mg}{k}\left(\sin\theta-\mu_c\cos\theta\right)\pm\sqrt{\frac{m^2g^2}{k^2}\left( \mu_c\cos\theta-\sin\theta\right)^2+\frac{2mg}{k}d\left(\sin\theta-\mu_c\cos\theta\right)}$$

Da forma que $\Delta x$ foi definida ela é uma quantidade restritamente positiva, então podemos desconsiderar o sinal negativo e obter,

$$\Delta x=\frac{mg}{k}\left(\sin\theta-\mu_c\cos\theta\right)+\sqrt{\frac{m^2g^2}{k^2}\left( \mu_c\cos\theta-\sin\theta\right)^2+\frac{2mg}{k}d\left(\sin\theta-\mu_c\cos\theta\right)}\ \ \ \ (5)$$

Substituindo os valores relacionados ao problema obtemos,

$$\Delta x=0,46m$$

b) Uma vez determinado a distância de compressão máxima da mola pela equação (5) podemos calcular o trabalho e obter a energia dissipada $E_d$ pelo sistema, já que $E_d=W$, pela equação (1) obtemos,

$$E_d=mg\mu_c\left( d+\Delta x\right)\cos\theta\ \ \ \ (6)$$

Substituindo os valores do problema obtemos que a energia dissipada foi,

$$E_d=85,2J$$

Podemos comparar a fração $F_d$ da energia dissipada pelo potencial gravitacional no início do movimento pela, que estão representados pelas equações (6) e (2) respectivamente,

$$F_d=\frac{E_i}{E_d}\Rightarrow$$
$$F_d=\frac{mg\mu_c\left( d+\Delta x\right)\cos\theta}{mg(d+\Delta x)\sin\theta}\Rightarrow$$
$$F_d=\mu_c\cot\theta$$

Substituindo o valor $\theta$ encontramos,

$$F_d=\mu_c$$

c)Usando o mesmo referencial adotado anteriormente, podemos examinar a força resultante $\vec{F}_r$ na direção $x$ para determinar se o bloco vai parar ou se será lançado para mais alto na rampa,

Usando a segunda lei de Newton obtemos as equações que descrevem as forças,

$$\left\lbrace \begin{array}{ll} N-P\cos\theta=0\ \ \ \ (7)\\ -F_a-P\sin\theta+F_e=F_r\ \ \ \ (8)\\ \end{array}\right.$$

Usando a equação (8) obtemos uma expressão para a força de atrito,

$$\vec{F}_r=-F_a\hat{i}-P\sin\theta\hat{i}+F_e\hat{i}\Rightarrow$$
$$\vec{F}_r=\left( -N\mu_e-mg\sin\theta+k\Delta x\right)\hat{i}$$
A normal é determinada pela equação (7)

$$\vec{F}_r=\left( -mg\cos\theta\mu_e-mg\sin\theta+k\Delta x\right)\hat{i}$$

Substituindo os valores obtemos

$$\vec{F}_r=\left( 243,2N\right)\hat{i}$$

Ou seja, o bloco será lançado para cima.