Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 7.19

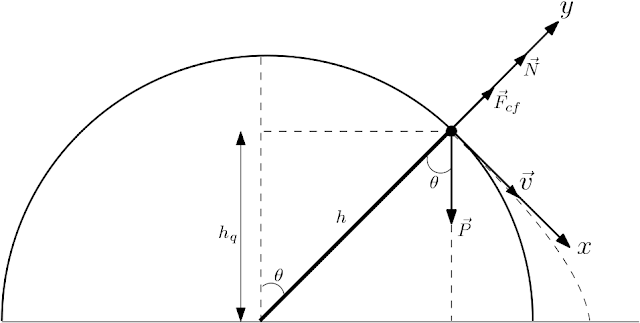
7,19) Um garotinho esquimó desastrado escorrega do alto do seu iglu, um domo hemisférico de gelo de 3 m de altura. (a) De que altura acima do solo ele cai? (b) A que distância da parede do iglu ele cai? a) Ao adotar o referencial no ponto que o esquimó perde o contato com o iglu de forma que o eixo $ox$ tangencie a semi semiesfera,

Podemos representar no referencial as forças que atuam sobre o esquimó no eixo $oy$ uma vez que é a parte do movimento que nos interessa, são elas a força centrifuga $\vec{F}_{cf}$, normal $\vec{N}$ e o peso $\vec{P}_y$ decomposto em $y$, como nessa direção o esquimó está em equilíbrio, a soma das forças resultantes nessa direção deve ser nula, $$N+F_{cf}-P_y=0$$ A partir do momento em que o esquino perde o contato com o iglu a força normal torna-se nula, logo, $$F_{cf}-P_y=0$$ , ou seja, $$m\frac{v^2}{h}-mg\cos\theta=0$$ Explicitando $v$ obtemos, $$v=\sqrt{hg\cos\theta}\ \ \ \ (1)$$ Podemos calcular a altura de queda atentando ao fato de que no momento que no esquimó perde o contato com o iglu ele tem energia cinética dada por (1) e energia potencial gravitacional dada por $h_q$ $$E_f=\frac{1}{2}mv^2+mgh_q$$ No primeiro momento ele tinha apenas energia potencial dada pela altura $h$, $$E_i=mgh$$ Como não foi perdido energia no processo teremos, $$E_f=E_i\Rightarrow$$ $$\frac{1}{2}mv^2+mgh_q=mgh$$ Substituindo a velocidade $v$ dada por (1) obtemos, $$\frac{1}{2}mhg\cos\theta+mgh_q=mgh$$ Explicitando $h_q$ obtemos, $$h_q=h\left(1-\frac{1}{2}\cos\theta\right) \ \ \ \ (2)$$ Olhando para o triângulo retângulo de lados adjacentes a $\theta$, $h$ e $h_q$, obtemos a seguinte relação, $$\cos\theta=\frac{h_q}{h}\Rightarrow$$ $$\cos\theta=1-\frac{1}{2}\cos\theta\Rightarrow$$ $$\frac{3}{2}\cos\theta=1\Rightarrow$$ $$\cos\theta=\frac{2}{3}\Rightarrow$$ $$\theta=\arccos\left( \frac{2}{3}\right)\Rightarrow$$ $$\theta=(48,18)°\ \ \ \ (3)$$ Aplicando (3) em (2) obtemos a altura de queda, $$h_q=2,01m$$ b). Podemos adotar o referencial com eixo $ox$ na direção horizontal, logo abaixo do ponto onde o esquimó perde o contato com o iglu,

Note que o esquimó cairá a uma distância $x_q=a+d$ da origem do referencial para prosseguir devermos encontrar o valor de $a$, podemos aplicar o teorema de Pitágoras no triângulo retângulo formado pela altura $h_q$ e base $x_0$ e obter $x_0=\sqrt{h^2+h_q^2}$, no entanto, como $h=x_0+a$ obtemos, $$a=h-\sqrt{h^2+h_q^2}\ \ \ \ (3)$$ Logo após perder o contato com o iglu o esquimó começa a descrever uma trajetória parabólica dada por, descrita pela equação, $$\left\lbrace \begin{array}{ll} x=v\cos\theta t\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)\\ y=h_q-v\sin\theta t -\frac{1}{2}gt^2\ \ (5)\\ \end{array}\right.$$ Devemos encontrar o tempo $t_q$ para o qual $y=0$, logo, pela equação (5) temos que, $$h_q-v\sin\theta t_q -\frac{1}{2}gt_q^2=0\Rightarrow$$ $$\frac{1}{2}t_q^2+\frac{v\sin\theta}{g}t_q-\frac{h_q}{g}=0$$ Resolvendo a equação de segundo gral obtemos, $$t_q=\frac{1}{g}\sqrt{v^2\sin^2\theta+2gh_q}-\frac{v\sin\theta}{g}$$ Aplicando $t_q$ na equação (4) obtemos $x_q$, $$x_q=\frac{v\cos\theta}{g}\left( \sqrt{v^2\sin^2\theta+2gh_q}-v\sin\theta \right)$$ Como já foi dito $x_q=a+d$, $$a+d=\frac{v\cos\theta}{g}\left( \sqrt{v^2\sin^2\theta+2gh_q}-v\sin\theta \right) \Rightarrow$$ $$d=\frac{v\cos\theta}{g}\left( \sqrt{v^2\sin^2\theta+2gh_q}-v\sin\theta \right)-a\Rightarrow$$ $$d=\frac{v\cos\theta}{g}\left( \sqrt{v^2\sin^2\theta+2gh_q}-v\sin\theta \right)-h+\sqrt{h^2+h_q^2}\ \ \ (6)$$ Substituindo os valores já encontrados do problema obtemos, $$d=0,36m$$