Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 6.14

6.14) Um pêndulo é afastado da vertical de um ângulo de $60°$ e solto em repouso. Para que ângulo com a vertical sua velocidade será a metade da velocidade máxima atingida pelo pêndulo?

 Adotando o referencial no nível potencial mais baixo do pendulo,

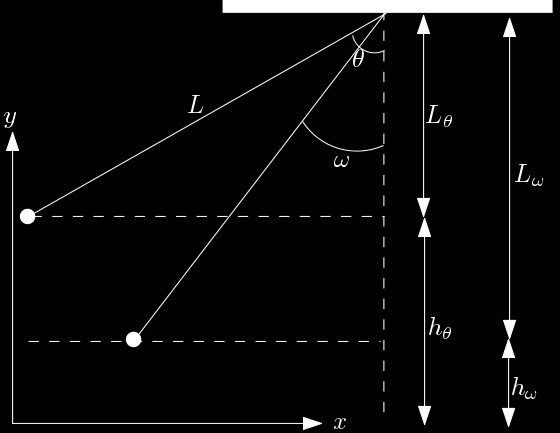
A velocidade máxima que o pendula atinge dado uma abertura $\theta$ é dada por, $$E_i=E_f\Rightarrow$$ $$mgh_\theta=\frac{1}{2}mv^2\Rightarrow$$ $$v=\sqrt{2gh_\theta}$$ Entretanto, $L=L_\theta+h_\theta$ enquanto $L_\theta=L\cos\theta$, logo teremos que, $$h_\theta=L\left(1-\cos\theta\right)$$ Aplicando o resultado na velocidade obtemos, $$v_\theta=\sqrt{2gL\left( 1-\cos\theta\right)}\ \ \ (1)$$ Queremos agora descobrir para qual ângulo $\omega$ durante o movimento a velocidade do pendulo será a metade da máxima $v_\theta$. Usando conservação de energia, no primeiro instante o pendulo tem apenas energia potencial, que durante o movimento é convertido em energia cinética, ou seja, $$mgh_\theta=\frac{1}{2}mv_\omega^2+mgh_\omega\ \ \ \ (2)$$ O comprimento do pendulo é $L=L_\omega+h_\omega$ para o ângulo $\omega$, da mesma forma vale a relação $L_\omega=L\cos\omega$, ou seja, $$L=L_\omega+h_\omega\Rightarrow$$ $$L=L\cos\omega+h_\omega\Rightarrow$$ $$h_\omega=L\left(1-\cos\omega\right)\ \ \ \ (3)$$ Substituindo (3) em (2) e lembrando que $v_\omega=\frac{1}{2}v_\theta$ obtemos $\omega$, $$mgL\left(1-\cos\theta\right)=\frac{1}{2}m\left( \frac{1}{2}v_\theta\right) ^2+mgL\left(1-\cos\omega\right)\Rightarrow$$ $$gL\left(1-\cos\theta\right)=\frac{1}{8}v_\theta^2+gL\left(1-\cos\omega\right)\Rightarrow$$ $$8gL-8gL\cos\theta=v_\theta^2+8gL-8gL\cos\omega\Rightarrow$$ $$\cos\omega=\cos\theta+\frac{v_\theta^2}{8gL}\Rightarrow$$ $$\omega=\arccos\left( \cos\theta+\frac{v_\theta^2}{8gL}\right)$$ Substituindo (1) na equação acima obtemos, $$\omega=\arccos\left( \cos\theta+\frac{2gL\left( 1-\cos\theta\right)}{8gL}\right)\Rightarrow$$ $$\omega=\arccos\left( \cos\theta+\frac{\left( 1-\cos\theta\right)}{4}\right)\Rightarrow$$ $$\omega=\arccos\left( \frac{3\cos\theta+1}{4}\right)\ \ \ \ \ (4)$$ No caso de um ângulo inicial $\theta=60°$ teremos que, $$\omega=\arccos\left( \frac{5}{8}\right)$$ Isto é, $$\omega=(51,3)°$$