Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.13

8.13) Num lançamento do foguete Saturno V (veja tabela da pg. 164) são queimadas $2.100$ toneladas de combustível em $2,5 min$, gerando um empuxo de $3,4\times10^7N$. A massa total do foguete com sua carga é de $2.800$ toneladas. (a) Calcule a velocidade de escape do combustível empregado. (b) Calcule a aceleração inicial do foguete na rampa de lançamento.

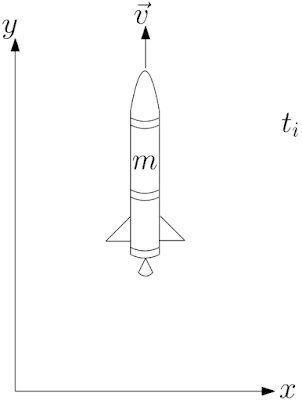
a) Supondo que o foguete já esteja no espaço onde a aceleração da gravidade pode ser desprezada no tempo $\Delta t$ de queima do combustível de massa $m_c$, representamos o foguete no momento inicial $t_i$ quando ainda não queimou nem um combustível tendo ele nesse momento uma massa $m$ e uma velocidade $\vec{v}$,

Nesse instante o seu momento $\vec{P}_i$ será, $$\vec{P}_i=m\vec{v}$$ Em um segundo momento $t_f$ o foguete ejeta uma quantidade de massa $\Delta m$ bem pequena a uma velocidade $\vec{u}$ em relação ao foguete, sendo tal velocidade medida no referencial em repouso como $\vec{v}-\vec{u}$, em consequência da perda de massa o foguete adquire um acréscimo na velocidade $\Delta \vec{v}$,

Nessas condições o momento final do foguete será, $$\vec{P}_f=\left( m-\Delta m\right)\left( \vec{v}+\Delta\vec{v}\right)+\Delta m\left( \vec{v}-\vec{u}\right)$$ Como por hipótese o momento é conservado teremos que, $$\vec{P}_i=\vec{P}_f\Rightarrow$$ $$m\vec{v}=\left( m-\Delta m\right)\left( \vec{v}+\Delta\vec{v}\right)+\Delta m\left( \vec{v}-\vec{u}\right)$$ Desenvolvendo a expressão obtemos, $$m\vec{v}=m\vec{v}+m\Delta\vec{v}-\Delta m\vec{v}+\Delta m\Delta\vec{v}+\Delta m\vec{v}-\Delta m\vec{u}\Rightarrow$$ $$\left( m\vec{v}-m\vec{v}\right) =m\Delta\vec{v}+\left(\Delta m\vec{v}-\Delta m\vec{v}\right) +\Delta m\Delta\vec{v}-\Delta m\vec{u}\Rightarrow$$ $$\Delta m\vec{u} =m\Delta\vec{v} +\Delta m\Delta\vec{v}$$ Podemos desprezar a quantidade $\Delta m\Delta\vec{v}$ e obter, $$m\Delta\vec{v}=\Delta m\vec{u}\ \ \ \ (1)$$ Dividindo tudo pelo tempo $\Delta t=t_f-t_i$ obtemos $$m\frac{\Delta\vec{v}}{\Delta t}=\frac{\Delta m}{\Delta t}\vec{u}$$ Dessa forma encontramos a força $\vec{F}_e$ que denominamos empuxo, $$\vec{F}_e=m\vec{a}=\frac{\Delta m}{\Delta t}\vec{u}\ \ \ \ (2)$$ Tomando a expressão em modulo e explicitando $u$ obtemos, $$u=\frac{F_e\Delta t}{\Delta m}$$ Substituindo os valores obtemos $$u=\frac{(3,4\times 10^7N)(150s)}{(2100\times 10^{3}kg)}\Rightarrow$$ $$u=2428m/s$$ ou $$u=2,428km/s$$ b) As forças que atuam sobre o sistema são o peso $P$ e a força de empuxo $F_e$ logo, $$\sum F=F_e-P=ma$$ Logo, $$a=\frac{F_e-mg}{m}$$ Substituindo os valores, $$a=\frac{(3,4\times 10^7kg)-(2,8\times 10^6kg)(9,8m/s^2)}{(2,8\times 10^6kg)}$$ Isto é, $$a=2,34m/s^2$$