Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.3

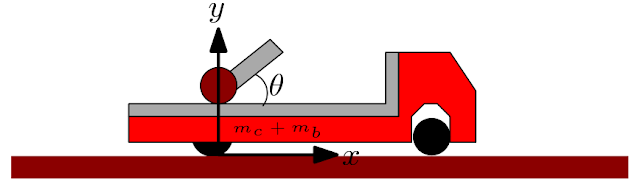
8.3) Um canhão montado sobre uma carreta, apontado numa direção que forma um ângulo de $(30)°$ com a horizontal, atira uma bala de $50kg$, cuja velocidade na boca do canhão é de $300m/s$. A massa total do canhão e da carreta é de $5$ toneladas. (a) Calcule a velocidade inicial de recuo da carreta. (b) Se o coeficiente de atrito cinético é $0,7$, de que distância a carreta recua? a) Podemos adotar o referencial no solo de forma que que ele permaneça em repouso em relação a carreta,

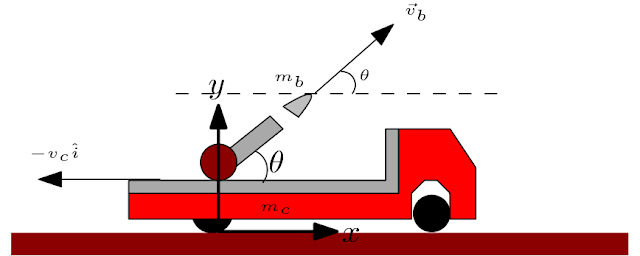
No primeiro momento o sistema está em repouso e o momento total é nulo, $\vec{P}_i=0$,

por outro lado, em um segundo momento a bala adquire uma velocidade $\vec{v}_b$ enquanto a carreta juntamente com o canhão recua com uma velocidade $-v_c\hat{i}$, podemos decompor o vetor velocidade da bala de forma a representar suas componentes vertical e horizontal segundo o referencial adotado, $$\vec{v}_b=v_b\cos\theta\hat{i}+v_b\sin\theta\hat{j}$$ Como estamos interessados apenas na componente horizontal do momento teremos que o momento final $\vec{P}_f$ será dado por, $$\vec{P}_f=m_bv_b\cos\theta\hat{i}-m_cv_c\hat{i}$$ Como o momento é conservado no processo teremos que, $$\vec{P}_i=\vec{P}_f\Rightarrow$$ $$0=m_bv_b\cos\theta\hat{i}-m_cv_c\hat{i}\Rightarrow$$ $$0=m_bv_b\cos\theta-m_cv_c$$ Explicitando $v_c$ obtemos, $$v_c=\frac{m_b}{m_c}v_b\cos\theta\ \ \ \ (1)$$ b) Usando o mesmo referencial podemos representar as forças que atuam sobre a carreta,

Podemos então representar usando a segunda lei de Newton as forças que atuam sobre a carreta, $$\left\lbrace\begin{array}{ll} \vec{N}+\vec{P}_c=0\\ \vec{F}_a=m_c\vec{a}\\ \end{array}\right.$$ Sendo assim a força de atrito é dada por, $$N\mu_c=-m_ca\Rightarrow$$ $$P_c\mu_c=-m_ca\Rightarrow$$ $$m_cg\mu_c=-m_ca\Rightarrow$$ $$a=-g\mu_c\Rightarrow$$ Sabendo que a carreta vai de $v_c$ a zero, com essa aceleração podemos usar a seguinte equação para encontra a distância percorria $\Delta x$, $$v_f^2=v_i^2+2a\Delta x\Rightarrow$$ $$0=v_c^2-2g\mu\Delta x\Rightarrow$$ $$v_c^2=2g\mu\Delta x\Rightarrow$$ $$2g\mu\Delta x=v_c^2\Rightarrow$$ $$\Delta x=\frac{v_c^2}{2g\mu}\ \ \ (2)$$ obtemos então o resultado (1) e (2), $$\left\lbrace \begin{array}{ll} v_c=\frac{m_b}{m_c}v_b\cos\theta\\ \Delta x=\frac{v_c^2}{2g\mu}\\ \end{array}\right.$$ Substituindo os valores do problema obtemos, $$\left\lbrace \begin{array}{ll} v_c=2,6m/s\\ \Delta x=0,49m\\ \end{array}\right.$$