Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.7

8.7) Um gafanhoto, pousado na beirada superior de uma folha de papel que está boiando sobre a água de um tanque, salta, com velocidade inicial de $4m/s$, em direção à beirada inferior da folha, no sentido do comprimento. As massas do gafanhoto e da folha são de $1g$ e de $4g$, respectivamente, e o comprimento da folha é de $30cm$. Em que domínio de valores pode estar compreendido o ângulo $\theta$ entre a direção do salto e a sua projeção sobre a horizontal para que o gafanhoto volte a cair sobre a folha? 

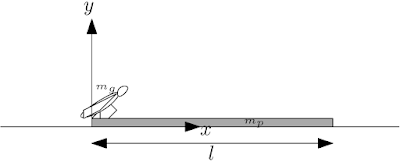
 Adotando o referencial sobre a superfície da água, podemos representar em relação a esse referencial o estado inicial do sistema,

Que consiste no grafanhoto de massa $m_g$ e o papel de massa $m_p$ parados em relação à água, logo, o momento será nulo,

Em um segundo momento quando o grafanhoto salta com velocidade $v_g$ com um ângulo $\theta$ em relação à horizontal, o papel será lançado com velocidade $v_p$ na direção $0x$ negativo. Note que, ao decompor a velocidade do grafanhoto obtemos que sua velocidade na direção horizontal é $v_{gx}=v_g\cos\theta$, dessa forma podemos supor que o momento na direção $ox$ é conservado, $$P_i=P_f\Rightarrow$$ $$0=m_gv_g\cos\theta-m_pv_p$$ Explicitando $v_p$ obtemos, $$v_p=\frac{m_g}{m_p}v_g\cos\theta\ \ \ \ (1)$$ Como o papel se move na direção $ox$ no sentido oposto ao movimento do grafanhoto, ele terá que levar em consideração essa velocidade para que possa pousar com segurança na outra ponta da folha de papel. Adotando o referencial sobre a folha de papel podemos perceber que o grafanhoto descreve uma trajetória parabólica dada por, $$\left\lbrace\begin{array}{ll} x=\left( v_{gx}+v_{p}\right)t\\ y=v_{gy}t-\frac{1}{2}gt^2(3)\\ \end{array}\right.$$ Ao utilizar a expressão (1) e decompor as velocidades, podemos escrever de forma mais explicita a equação do movimento do grafanhoto, $$\left\lbrace\begin{array}{ll} x=v_{g}\cos\theta\left(1+\frac{m_g}{m_p}\right)t\ \ \ \ (2)\\ y=v_{g}\sin\theta t-\frac{1}{2}gt^2\ \ \ \ (3)\\ \end{array}\right.$$ Note que o movimento em $ox$ (equação 2) é crucial para o grafanhoto, como é um movimento uniforme, queremos descobrir qual será o tempo $t_q$ em que $x=l$, logo, $$l=v_{g}\cos\theta\left(1+\frac{m_g}{m_p}\right)t_q\Rightarrow$$ $$t_q=\frac{l}{v_{g}\cos\theta\left(1+\frac{m_g}{m_p}\right)}$$ Uma vez descoberto o tempo $t_q$ em que o grafanhoto permanece no ar, a equação (3) deve ter solução nula (y=0) para o tempo $t_q$, logo, $$0=v_{g}\sin\theta t_q-\frac{1}{2}gt_q^2\Rightarrow$$ $$0=v_{g}\sin\theta-\frac{1}{2}gt_q\Rightarrow$$ $$0=v_{g}\sin\theta-\frac{lg}{2v_{g}\cos\theta\left(1+\frac{m_g}{m_p}\right)}\Rightarrow$$ $$2\cos\theta\sin\theta=\frac{lg}{v_{g}^2\left(1+\frac{m_g}{m_p}\right)}\Rightarrow$$ $$\sin2\theta=\frac{lg}{v_{g}^2\left(1+\frac{m_g}{m_p}\right)}\Rightarrow$$ $$\theta=\frac{1}{2}\arcsin\left( \frac{lg}{v_{g}^2\left(1+\frac{m_g}{m_p}\right)}\right)$$ Substituindo os valores obtemos, $$\theta=(4,2)°$$ Logo o grafanhoto pode pular com inclinação $0\leqslant\theta\leqslant(4,2)°$ e ainda cair sobre a folha de papel, porém, existe outro valor que satisfaz $\sin2\theta$ que é $\sin2\left( \theta+90°\right)$ logo acima do ângulo, $$\theta=\frac{1}{2}\arcsin\left( \frac{lg}{v_{g}^2\left(1+\frac{m_g}{m_p}\right)}\right)-90°\Rightarrow$$ $$\theta=(85,7)°$$ Dessa forma  os intervalos validos para o salto do grafanhoto de modo que ele caia sobre a folha de papel são $0\leqslant\theta\leqslant(4,2)°$ e $(85,7)°\leqslant\theta\leqslant90°$.