Moyses - Curso de Física Básica, Mecânica, Problema Resolvido 8.14

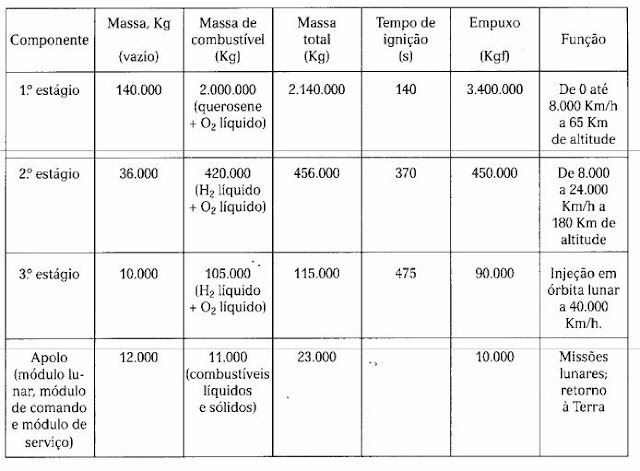
8.14) Utilizando os dados da tabela da pg. 164, calcule, para o 3° estágio do sistema Saturno V-Apolo: (a) a velocidade de escape dos gases de combustão; (b) o incremento de velocidade produzido por este estágio, na ausência de forças externas. A diferença entre o resultado e os valores da tabela pode ser atribuída a essas forças (gravidade e resistência atmosférica residuais).

a) Como foi feito no exercício 8.13, a velocidade de escape do combustível $v_e$ é dado em termos da massa ejetada $\Delta m$, a massa total no momento do terceiro estágio $m_{T3}$ e a variação de velocidade do foguete $\Delta v$, $$-\Delta m v_e=m_{t3}\Delta v\ \ \ (1)$$ Dividindo a expressão pelo tempo de ejeção obtemos, $$-\frac{\Delta m}{\Delta t} v_e=m_{t3}\frac{\Delta v}{\Delta t}$$ A parte direita da equação é a força de empuxo $F_e$ logo, $$-\frac{\Delta m}{\Delta t} v_e=F_e$$ Explicitando $v_e$ obtemos, $$v_e=-\frac{F_e\Delta t}{\Delta m}$$ Olhando para a tabela no terceiro estágio podemos ver que $F_e=90000kgf=882598,5N$ o tempo de ejeção é $\Delta t=475s$ enquanto que a massa do combustível ejetado é $\Delta m=105\times10^3kg$ substituindo os valores obtemos $$v_e=-\frac{(882598,5N)(475s)}{(105\times10^3kg)}\Rightarrow$$ $$v_e=-3992,7m/s$$ Ou, $$v_e=-3,9927km/s$$ b) Tomando as quantidades infinitesimais da equação (1) obtemos, $$-d m v_e=md v\Rightarrow$$ $$-\frac{1}{m}d m v_e=d v$$ Integrando a expressão, $$-\int_{m_i}^{m_f}\frac{1}{m}d m v_e=\int_{v_i}^{v_f}d v\Rightarrow$$ $$-v_e\ln\left( \frac{m_f}{m_i}\right)=v_f-v_i\Rightarrow$$ $$\Delta v=v_f-v_i=v_e\ln\left( \frac{m_i}{m_f}\right)\ \ \ \ (2)$$ No caso do primeiro estagio, supondo que o foguete parta do repouso, $$v_{f1}=v_e\ln\left( \frac{m_T}{m_T-m_{c1}}\right)$$ Onde $m_{c1}$ é a massa do combustível do estágio 1. Para o segundo estágios, $$v_{f2}-v_{f1}=v_e\ln\left( \frac{m_T-m_{01}-m_{c1}}{m_T-m_{c1}-m_{01}-m_{c2}}\right)$$ Onde $m_{c2}$ é a massa do combustível do estágio 2 e $m_{01}$ é a massa do estágio vazio 1. Para o terceiro estágio teremos $$v_{f3}-v_{f2}=v_e\ln\left( \frac{m_T-m_{01}-m_{c1}-m_{c2}-m_{02}}{m_T-m_{c1}-m_{01}-m_{c2}-m_{02}-m_{c3}}\right)$$ Onde $m_{c3}$ é a massa do combustível do estágio 3, onde $m_{02}$ é a massa do estágio 2. Somando a massa de todos os estágios, obtemos $m_T=2734000$, logo, $$m_T-m_{01}-m_{c1}-m_{c2}-m_{02}=138000kg$$ Enquanto, $$m_T-m_{c1}-m_{01}-m_{c2}-m_{02}-m_{c3}=33000kg$$ A velocidade de ejeção foi calculado na questão (a) $v_e=4km/s=14400km/h$, como queremos o acréscimo de velocidade usaremos $\Delta v$, $$\Delta v=\left( 14400km/h\right) \ln\left( \frac{\left( 138000kg\right) }{\left( 33000kg\right) }\right)\Rightarrow$$ $$\Delta v=20602,7km/h$$